
¶ Un peu de dessins !
Pour la suite des exercices, nous utiliserons le module turtle permettant de tracer de nombreuses figures géométriques.
Pour importer le module, il suffit d'ajouter la ligne suivante.
import turtle
Vous avez accès à l'ensemble de la documention avec ce lien : https://docs.python.org/fr/3/library/turtle.html#turtle.goto
Le principe est simple : on peut déplacer un petit robot permettant de dessiner des formes. La position par défaut du robot est [0;0]. On peut ensuite effectuer plusieurs opérations :
- Avancer :
forward(100)dessine une ligne de 100 px. - Pivoter à droite :
right(90)fait pivoter le robot de 90° vers la droite. - Pivoter à gauche :
left(90)fait pivoter le robot de 90° vers la gauche.
Voici un exemple de code pour dessiner un carré :
def carre():
for i in range(4):
turtle.forward(100)
turtle.right(90)
carre()
done()
Remarque : La ligne done() doit toujours être présente à la fin de votre programme.
¶ Exercice 1
Question 1 - Pour tester, écrire un programme permettant de dessiner la figure suivante.
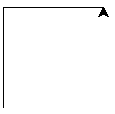
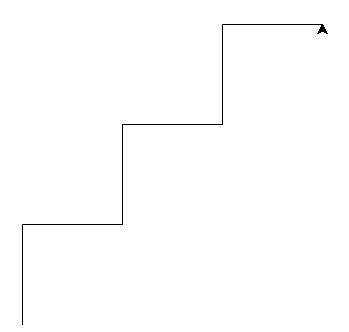
Question 2 - Écrire une fonction récursive escalier qui prend un nombre de marche en paramètre. Cette fonction construit un escalier à marche(s).
¶ Exercice 2
Question 1 - Écrire une fonction polygone qui prend en paramètre un nombre de côté et une longueur. Cette fonction dessine un polygone régulier de côtés de longueur .
polygone(4,100)dessine un carré de 100px de longueur.polygone(8,50)dessiner un octogone de 50px de longueur.
def polygone(n, longueur):
'''
:param n: Le nombre de cöté
:param longueur: La longueur d'un côté
'''
pass
Question 2 - Réécrire la fonction ci-dessus de manière récursive.
def polygone_recursif(n, longueur):
'''
:param n: Le nombre de côté
:param longueur: La longueur d'un côté
'''
pass
¶ Exercice 3 - Des spirales !
Question 1 - Écrire une fonction spirale_carre qui prend en paramètre une longueur. Cette fonction permet de dessiner une spirale carrée de taille . Cette fonction ne s'arrête pas.
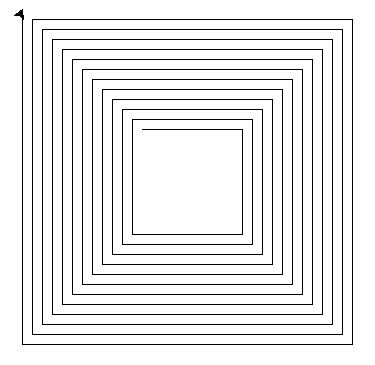
def spirale_carre(longueur):
'''
:param longueur: (int) La longueur du carré de départ
'''
Question 2 - 2. Écrire une fonction spirale qui prend en paramètre une longueur et un angle. Cette fonction permet de dessiner une spirale de taille . La forme de la spirale est indiquée grâce à l'angle de 2 côtés du polygone.
- Exemple :
spirale(100,120)

- Exemple :
spirale(5,89)

def spirale(longueur, angle):
'''
:param longueur: (int) La longueur du carré de départ
:param angle: (int) L'angle formé par 2 côtés du polygone
'''
pass
¶ Exercice 4 - Les triangles de Sierspinski
Le triangle de Sierpinski est une figure géométrique qui repose sur le concept de la récursivité. L'objectif de cet exercice est de réaliser une fonction permettant de dessiner ces triangles.

¶ Principe de construction
L’algorithme divise un triangle « père » ABC dont les sommets ont pour coordonnées A(xA,yA), B(xB,yB) et C(xC,yC), en quatre triangles : 3 triangles « fils » AEG, EBF, GFC et un triangle central EFG où :
- E désigne le milieu de [AB]
- F le milieu de [BC]
- G le milieu de [AC].
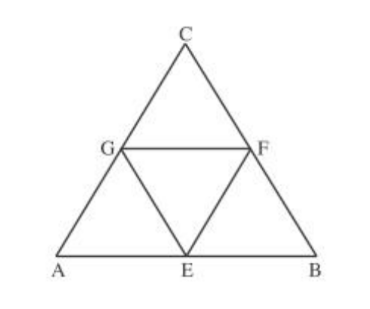
Ensuite, il recommence l’opération pour tous les triangles « fils ».
C'est ici qu'intervient le processus récursif. Vous pouvez observer la création du triangle à l'aide de cette vidéo :

¶ Construction
Pour réaliser cette animation, nous avons donc besoin de 3 fonctions :
- Une fonction
milieu(a,b)qui retourne le milieu du segment[a,b]. - Une fonction
dessiner_triangle(a,b,c)selon 3 points passés en paramètre. - Une fonction
sierpinski(a,b,c,profondeur)qui lance le tracé du triangle de Sierpinski. C'est cette fonction qui sera récursive.
Question 1 - À l'aide de la documentation de turtle, écrire la fonction dessiner_triangle. Elle prend en paramètre une couleur sous la forme d'une chaine de caractère, et 3 tuples représentants la position (x, y) des 3 sommets du triangle.
def dessiner_triangle(color:str, a:int, b:int, c:int):
pass
def dessiner_triangle(color,a,b,c):
turtle.fillcolor(color)
turtle.up()
turtle.goto(a)
turtle.down()
turtle.begin_fill()
turtle.goto(b)
turtle.goto(c)
turtle.goto(a)
turtle.end_fill()
Question 2 - Écrire la fonction milieu. Cette fonction prend en paramètre 2 tuples représentant les coordonnées de deux points. Elle retourne un tuple correspondant aux coordonnées du point au milieu du segment[a, b].
def milieu(a:tuple, b:tuple):
pass
def milieu(a,b):
'''
:param a: (tuple) Position du 1er point
:param b: (tuple) Position du 2ème point
:return: (tuple) Milieu du segment
'''
x = (a[0]+b[0])/2
y = (a[1]+b[1])/2
return (x,y)
Question 3 - Écrire une fonction récursive sierpinski(a,b,c,profondeur) qui lance le tracé du triangle de Sierpinski. Pour vous aider, voici une explication de l'algorithme :
DessinerTriangle(A,B,C)sierpinski(A, Milieu(A,B), Milieu(A,C), ..........)sierpinski(.................................)sierpinski(.................................)
import turtle
def dessiner_triangle(color,a,b,c):
turtle.fillcolor(color)
turtle.up()
turtle.goto(a)
turtle.down()
turtle.begin_fill()
turtle.goto(b)
turtle.goto(c)
turtle.goto(a)
turtle.end_fill()
def milieu(a,b):
'''
:param a: (tuple) Position du 1er point
:param b: (tuple) Position du 2ème point
:return: (tuple) Milieu du segment
'''
x = (a[0]+b[0])/2
y = (a[1]+b[1])/2
return (x,y)
def sierpinski(a:tuple, b:tuple, c:tuple, n:int):
couleurs=['blue', 'red', 'green', 'white', 'black','yellow','purple']
if n > 0:
dessiner_triangle(couleurs[n],a,b,c)
sierpinski(a,milieu(a,b), milieu(a,c), n-1)
sierpinski(milieu(a,b), b, milieu(b,c),n-1)
sierpinski(milieu(a,c), milieu(b,c), c,n-1)
a = (0, 200)
b = (-173, -100)
c = (173, -100)
profondeur = 3 # Profondeur désirée
sierpinski(a, b, c, 3)
¶ Exercice 5 - Dessinons des arbres !
Question 1 - Écrire une fonction récursive arbre(hauteur, profondeur, angle) qui permet de dessiner des arbres. Ce schéma ci-dessous vous permet de comprendre l’utilité de chacun de ses paramètres :
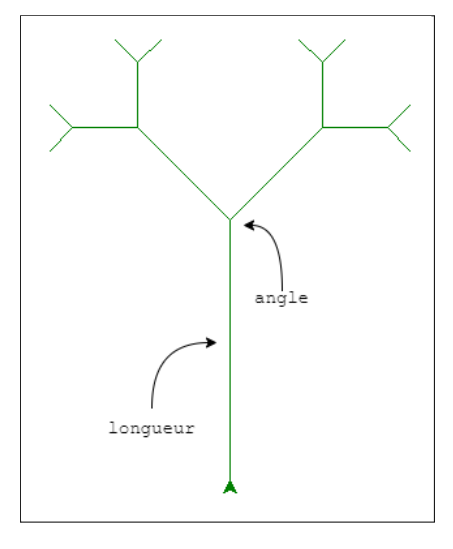
def arbre( hauteur:int, profondeur:int, angle:int ) :
'''
:param hauteur: Taille du tronc de l'arbre
:param profondeur: Profondeur de l'arbre
:param angle:
'''
pass
Voici des exemples de fonctionnement de cette fonction :
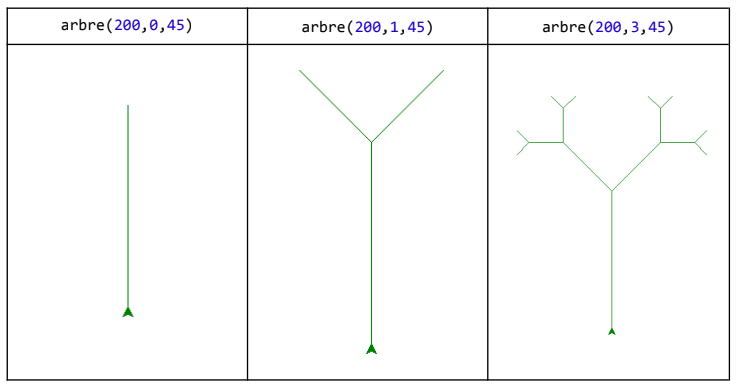
Question 2 - Essayer cette fonction en changeant les paramètres de la fonction (angle = 90, angle = 120).
¶ Exercice 6 - L'arbre de Pythagore
Question 1 - Écrire une fonction récursive pythagore(cote, profondeur) qui permet de dessiner un arbre de Pythagore.

def pythagore(cote:int, profondeur:int):
'''
:param cote: Taille du carre
:param profondeur: Profondeur de l'arbre
'''
pass
Vous trouverez ci-dessous quelques informations pour vous aider à réaliser cette fonction :
- Une méthode pour dessiner un carré avec une couleur aléatoire :
def dessiner_carre(cote) :
turtle.pencolor(randint(0,255), randint(0,255), randint(0,255))
turtle.fillcolor(randint(0,255), randint(0,255), randint(0,255))
turtle.begin_fill()
for _ in range(4) :
turtle.forward(cote)
turtle.right(90)
turtle.end_fill()
- Pour chaque profondeur, la taille des côtés du carré est égale à :
cote = longueur / racineCarre(2) - Voici une vidéo au ralenti permettant de dessiner un arbre de profondeur 4.