
¶ Exercice 1 - La suite de Fibonacci
Dans cet exercice, on s'intéresse à l'optimisation de l'algorithme de la suite de Fibonacci.
¶ Partie 1 - Algorithme récursif
La suite de Fibonacci est définie comme suit :
Question 1 - Écrire une fonction récursive fibo() permettant de calculer la suite de Fibonacci.
def fibo(n:int) -> int:
return
Pour n=6, il est possible d'illustrer le fonctionnement de ce programme avec le schéma ci-dessous :
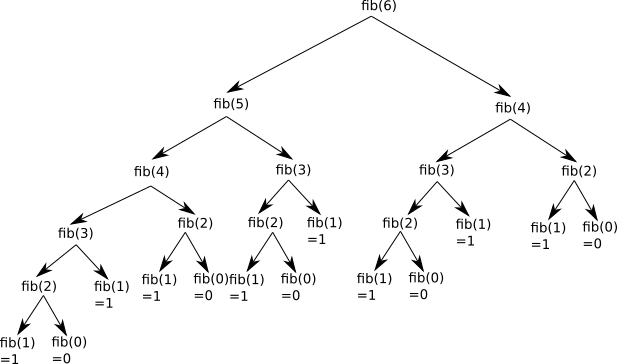
Pour les algorithmes récursifs, on peut représenter chaque appel sous la forme d'un arbre. Sur ce schéma, si on additionne toutes les feuilles de cette structure arborescente fib(1)=1 et fib(0)=0), on retrouve bien 8.
En observant attentivement le schéma ci-dessus, on peut remarquer que de nombreux calculs sont inutiles, car ils sont effectués 2 fois. Par exemple, on retrouve le calcul de fib(4) à 2 endroits :
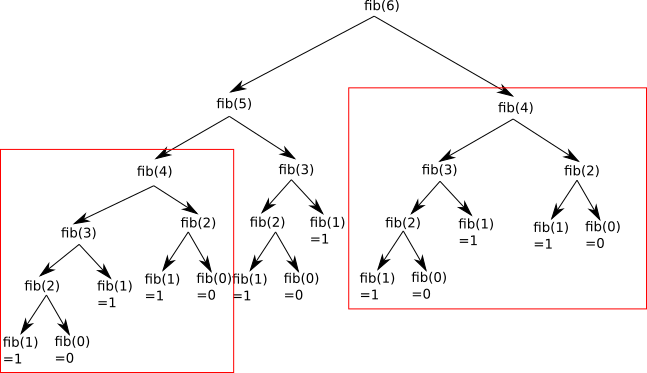
Il est donc possible de simplifier le calcul en exécutant une seule fois fib(4) et en mémorisant le résultat afin de le réutiliser quand c'est nécessaire.
¶ Partie 2 - La programmation dynamique
La programmation dynamique résout des problèmes en combinant des solutions optimales de sous-problèmes. Cette méthode a été introduite au début des années 1950 par Richard Bellman. Elle s'applique lorsqu'on rencontre des sous-problèmes identiques.
Par exemple, pour le cas du calcul de fib(6), on doit calculer 2 fois fib(4). Pour calculer fib(4), on doit calculer 4 fois fib(2)....
Un algorithme de programmation dynamique résout chaque sous-problème une seule fois et mémorise le résultat dans un tableau, évitant ainsi de recalculer la solution chaque fois qu'il résout chaque sous-sous-problème.
Utilisons cette méthode pour optimiser l'algorithme de la suite de Fibonacci.
¶ La méthode descendante (Top-Down)
Dans cette situation, nous utilisons l'approche dite « descendante (Top-Down) ». On commence par le problème global et on découpe en sous-problèmes récursivement.
Pour écrire un programme qui utilise cette méthode, on considère les deux fonctions suivantes :
def fibo_dyn_descendante(n):
memoire = [0] * (n+1)
memoire[0] = 0
memoire[1] = 1
return fibo_memoire(n, memoire)
def fibo_memoire(n, memoire):
# À compléter
return
La fonction fibo_dyn_descendante permet de générer un tableau dans lequel seront stockés les différents résultats des sous-problèmes. Ce tableau est transmis à la fonction fibo_memoire qui permet d'obtenir le résultat de manière récursive.
Question 1 - Écrire la fonction fibo_memoire. Cette fonction prend en paramètre un entier et une liste stockant les différents résultats des sous problèmes.
Cette fonction utilisera cette liste pour aller rechercher un résultat si celui-ci a déjà été calculé auparavant. Si le résultat n'est pas présent, le calcul sera effectué, et son résultat sera ajouté à la liste.
¶ La méthode ascendante (Bottom-Up)
Dans cette situation, nous utilisons l'approche dite « ascendante (Bottom-Up) ». On commence par résoudre les sous-problèmes les plus petits et on utilise leurs résultats pour résoudre progressivement des problèmes plus grands jusqu'à obtenir la solution au problème principal.
Question 2 - Écrire la fonction fibo_dyn_ascendante. Cette fonction prend en paramètre un entier n et fonctionne de la même manière que la fonction fibo_dyn_descendante. Elle utilisera une boucle au lieu d'utiliser les appels récursifs. Voici le début de la fonction.
def fibo_dyn_ascendante(n):
if n ==0:
return ...
if n == 1 :
return ...
memoire = ...
memoire[0] = ...
memoire[1] = ...
...
¶ Partie 3 - Performances
Le code ci-dessous permet de tester l'efficacité temporelle des deux méthodes.
import timeit
x1 = timeit.timeit(setup="from __main__ import fibo",stmt='fibo(25)',number=1000)
print(x1)
x2 = timeit.timeit(setup="from __main__ import fibo_dyn_descendante",stmt='fibo_dyn_descendante(25)',number=1000)
print(x2)
x3 = timeit.timeit(setup="from __main__ import fibo_dyn_ascendante",stmt='fibo_dyn_ascendante(25)',number=1000)
print(x3)
Question 3 - Ajouter le code ci-dessus afin de voir le gain de performance des fonctions fibo_dyn_ascendante et fibo_dyn_descendante
¶ Exercice 2 - Le rendu de monnaie
Dans l'activité 1, nous avons déjà travaillé sur le problème du rendu de monnaie. En utilisant les algorithmes gloutons, certaines solutions trouvées n'étaient pas optimales, et d'autres n'étaient pas exactes. La programmation dynamique va pouvoir résoudre cette problématique.
¶ Rappel
Dans ce problème, on retrouve un système monétaire et une certaine somme à rendre. Le problème est le suivant : « Quel est le nombre minimum de pièces qui doivent être utilisées pour rendre la monnaie ».
La résolution gloutonne de ce problème peut être la suivante :
- on prend la pièce qui a la plus grande valeur. Il faut que la valeur de cette pièce soit inférieure ou égale à la somme restant à rendre.
- On recommence l'opération ci-dessus jusqu'au moment où la somme à rendre est égale à zéro.
Intéressons-nous une version récursive de cet algorithme. Au début, on ne s'intéressera qu'au nombre de pièces minimum à obtenir.
¶ Un algorithme récursif
Question 1 - Écrire la fonction récursive rendu_monnaie_rec. Elle prend en paramètre un système de pièce sous la forme d'une liste d'entier et une somme à rendre. Elle renvoie le nombre de pièces permettant de rendre la somme en paramètre. Voici le détail de l'algorithme :
- Choisir le cas de base (par exemple, pour une somme à rendre égale à 0 )
- On essaie toutes les pièces possibles.
- Pour chaque pièce
systeme[i], on calcule récursivement le nombre de pièces poursomme - systeme[i] - On garde le minimum de toutes ces options.
- Pour chaque pièce
def rendu_monnaie_rec(systeme, somme
print("exécution avec somme=", somme) #Laisser la ligne
pass
Question 2 - Tester la fonction rendu_monnaie_rec en exécutant les lignes suivantes :
systeme = [2,5,10,50,100]
nb = rendu_monnaie_rec(systeme, 11 )
print('Nombres de pièces utilisées classique :',nb)
Question 3 - Que pouvons-nous remarquer suite à l'affichage de tous les appels récursif ?
¶ Analyse de l'algorithme récursif
Voici un schéma (avec une somme à rendre de 11 €) qui permet de mieux comprendre le principe de cette fonction :
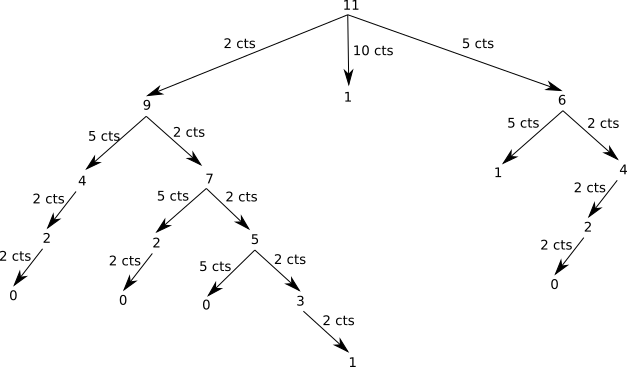
Plusieurs remarques s'imposent :
- Comme vous pouvez le remarquer sur le schéma, tous les cas sont traités. On appelle cela la méthode « brute force ».
- Pour certains cas, on peut se retrouver dans une impasse. Dans cette situation, la fonction renvoie
infce qui permet de s'assurer que cette solution ne sera pas retenue. - La profondeur minimum de l'arbre, avec une feuille à 0, est de 4. La solution au problème est donc 4 pièces.
Question 4 - Essayer le problème avec les sommes à rendre suivantes : 11, 36, 61, 78, 93, 117,171
Comme vous pouvez le constater, le programme ne permet pas d'obtenir une solution pour des grosses sommes. Pourquoi ? Parce que les appels récursifs sont trop nombreux et l'on dépasse la capacité de la pile d'exécution.
Cette méthode ne permet pas d'obtenir un résultat rapidement.
Le gos inconvénient de cette méthode est qu'elle souffre de chevauchements de sous-problèmes, ce qui entraîne une complexité exponentielle. Comme vous avez peut-être déjà dû le remarquer, nous faisons plusieurs fois exactement le même calcul. Par exemple, on retrouve 2 fois la branche qui part de 4 :
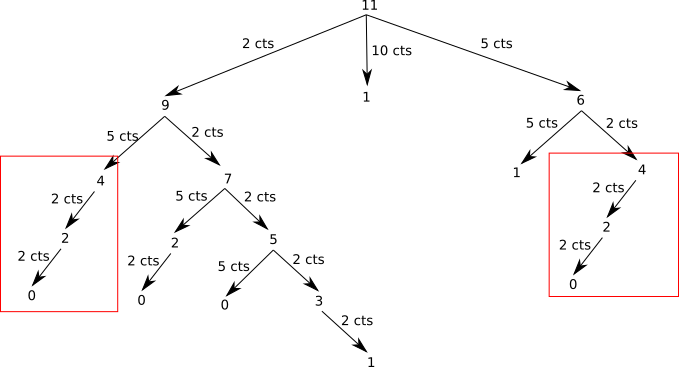
Il est donc possible d'appliquer la méthode de la programmation dynamique !
¶ La programmation dynamique
La programmation dynamique permet ici de stocker les résultats intermédiaires.
On retrouve la même fonction que dans l'exercice 1, qui utilise une approche descendante (Top-Down).
def rendu_monnaie_descendante(systeme, somme):
memoire = ...
return ...
def rendu_monnaie_memoire(systeme, somme, memoire):
return
Dans ce cas, la mémoire est une liste d'entier permettant de stocker le nombre de pièces minimales.
Question 5 - Sur le même principe que l'exercice 1, compléter la fonction rendu_monnaie_descendante. La fonction retourne un entier représentant le nombre de pièces.
Question 6 - Essayer le programme suivant.
systeme = [2,5,10,50,100]
r, l= rendu_monnaie_dyn(systeme, 171)
print('Liste des pièces utilisées prog dyn :',l)
Maintenant, le résultat s'obtient en quelques milisecondes alors qu'il était impossible d'obtenir un résultat en un temps résonnable avant.
Question 7 - Essayer d'écrire la fonction rendu_monnaie_ascendante, qui utilise une approche ascendante, (Bottom-Up). On utilisera un tableau pour stocker les résultats intermédiaires.
def rendu_monnaie_ascendante(systeme, somme_a_rendre):
memoire = [ float('inf') for _ in range(somme_a_rendre+1) ]
memoire[0] = [ 0]
¶ Performances
Le code ci-dessous permet de tester l'efficacité temporelle des deux fonctions.
import timeit
x1 = timeit.timeit(setup="from __main__ import rendu_monnaie_rec",stmt='rendu_monnaie_rec([2,5,10,50,100],45)',number=1000)
print(x1)
x2 = timeit.timeit(setup="from __main__ import rendu_monnaie_ascendante",stmt='rendu_monnaie_ascendante([2,5,10,50,100],45)',number=1000)
print(x2)
Question 8 - Ajouter le code ci-dessus afin de voir le gain de performance de la fonction rendu_monnaie_dyn qui utilise la programmation dynamique.
¶ Conclusion
Pour conclure le problème du rendu de monnaie, utilisons le système monétaire britannique afin de rendre la somme de 49 €. Cette situation était problématique lorsqu'on utilisait un algorithme glouton (voir activité 1).
Question 8 - Modifier vos fonctions rendu_monnaie_ascendante et rendu_monnaie_descendante afin de renvoyer également la liste de pièces utilisées.
Question 9 - Utiliser les fonctions précédente et le système monétaire britannique pour obtenir la liste de pièces nécessaires pour rendre 49 €.
Cette fois, le résultat obtenu est optimale avec la liste de pièces
l = [1, 24, 24].
¶ Exercice 3 - L'optimisation de découpe d'une corde
Un magasin achète des cordes d'escalade de longueur et les découpe en cordes plus petites pour les vendre à ses clients. On souhaite déterminer un découpage optimal pour maximiser le revenu, sachant que les prix de vente d'une corde de x mètres sont donnés ci-dessous.
| taille | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| prix | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 18 | 20 | 24 | 26 |
Dans notre exercice, on suppose que l'on dispose d'une corde de taille L=10
On considère également la liste des prix et des tailles :
taille = [0,1,2,3,4,5,6,7,8,9,10]
prix = [0,1,5,8,9,10,17,18,20,24,26]
¶ Algorithme glouton
Pour cette première étape, on décide d'écrire une version gloutonne de l'algorithme en se basant sur le calcul de « la densité » d'une corde. La densité d'une corde correspond à au rapport entre le prix et la taille, c'est-à-dire son prix au mètre.
Question 1 - Écrire une fonction generer_densite. Elle prend en paramètre les deux tableaux taille et prix. Elle retourne une liste de tuple selon le format suivant : (taille, prix, rapport)
Question 2 - En utilisant une méthode gloutonne, écrire une fonction decoupe_gloutonne. Cette fonction prend en paramètre la taille totale de la corde, la liste des prix et des tailles. Elle renvoie un tuple composé de la longueur totale découpée et un dictionnaire associant chaque segment de découpe à son nombre.
def decoupe_gloutonne(l:int, prix:list, taille:list) -> tuple :
pass
Question 2 - Donner le gain possible pour une corde de taille L=4. Est-ce la situation optimale ?
¶ Algorithme brute force
À partir de maintenant, on ne cherche plus à connaître l'ensemble de découpe qui conduit à la somme maximale. On se contente de chercher cette somme.
La méthode de brute force consiste à tester toutes les possibilités de solution et de récupérer la meilleure. Pour cela, on souhaite écrire une fonction récursive basé sur la relation de récurrence suivante :
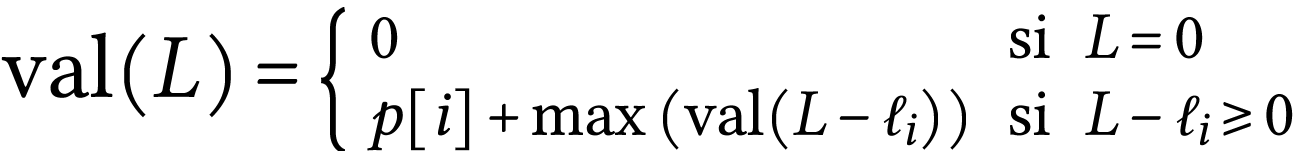
Question 3 - Écrire la fonction récursive decoupe_force_brute. Cette fonction prend en paramètre la taille totale de la corde, la liste des prix et des tailles. Elle renvoie la somme maximale des découpes que l'on peut effectuer.
def decoupe_brute_force(l:int, prix:list, taille:list) -> int :
pass
La stratégie par force brute nous apprend que l'on peut gagner 10. Par contre, cette solution n'est pas utilisable avec de grand nombre car beaucoup trop de calculs.
¶ Algorithme de programmation dynamique
Nous allons sauvegarder les résultats de calculs intermédiaires afin d'éviter de faire des calculs identiques plusieurs fois.
Question 4 - Compléter les fonctions suivantes afin de calculer la somme maximale des découpes que l'on peut effectuer en utilisant la programmation dynamique.
def decoupe_dyn_descendante(l:int, prix:list, taille:list) :
return
def memoisation (l:int, prix:list, taille:list, dico) -> int:
return
Vous devez obtenir le même résultats que la méthode par brute force pour
L=4. Seulement, cet algorithme est plus efficace et permet d'utilise de grande longueur de corde.
Question 5 - Proposer une fonction decoupe_dyn_ascendante qui utilise une approche ascdendante pour trouver une solution. On utilisera un tableau afin de stocker tous les calculs intermédiaires, en partant du plus petit sous-problème.
def decoupe_dyn_ascendante(l:int, prix:list, taille:list) :
return
Question 6 - Tester l'efficacite des 3 méthodes (gloutonne, brute force et programmation dynamique) à l'aide du module timeit.