
¶ Partie 1
¶ Partie 2
¶ Exercice 1 - Classe GraphePondere
Avant de s'intéresser à l'algorithme de Dijkstra, il faut construire une classe GraphePondere qui hérite de la classe Graphe.
Question 1 - Dans un fichier GraphePondere.py, écrire une classe GraphePondere qui hérite de la classe Graphe.
- Les paramètres du constructeur sont identiques à la classe
Graphe. - On ajoutera un attribut
ponderation. Cet attribut sera un dictionnaire qui associe une arête à une pondération. Les arêtes sont représentées sous la forme d'un tuple(s1, s2).
Question 2 - Redéfinir la méthode ajouter_arete. La méthode prend un paramètre supplémentaire de type entier et représente la pondération de l'arête.
def ajouter_arete(self, s1, s2, ponderation) -> None:
pass
Question 2 - Redéfinir la méthode show. Cette méthode affiche maintenant la pondération associée à chaque arête. Chaque sommet est affiché sous la forme d'un tuple avec son nom et sa pondération. Voici un exemple d'affichage :
A -> (B,7)(D,15)
B -> (A,7)(C,12)(F,16)(E,4)
C -> (B,12)(D,5)(F,3)
D -> (A,15)(C,5)(E,2)
E -> (B,4)(D,2)(F,14)
F -> (B,16)(C,3)(E,14)
Question 3 - Redéfinir la méthode voisins. Cette méthode retourne la liste des voisins du sommet passé en paramètre. Chaque voisin sera sous la forme d'un tuple composé de la lettre et sa pondération par rapport au sommet.
def voisins(self,sommet):
pass
Question 4 - Écrire la méthode get_ponderation. Cette méthode prend en paramètre deux sommets sous la forme d'une chaîne de caractères. Elle retourne la pondération associé à cette arête.
def get_ponderation(self, s1, s2) -> int :
pass
Question 5 - Pour tester votre programme, créer une instance de la classe GraphePondere. On utilisera l'exemple de l'activité 4.
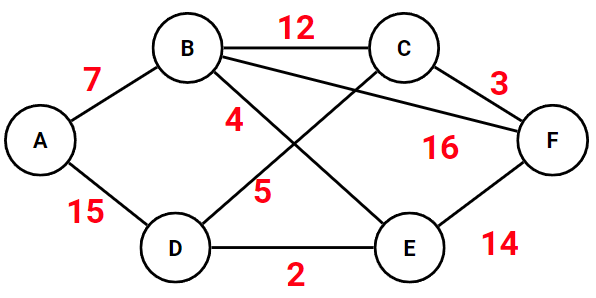
Pour la suite, on essayera de trouver le plus court chemin entre les sommets A et F.
¶ Exercice 2 - Classe Dijkstra
Pour regrouper toutes les méthodes liées à l'algorithme, on utilise une classe Dijkstra.
Question 1 - Créer un fichier Dijkstra.py.
Question 2 - Dans ce fichier, écrire une classe Dijkstra. Le constructeur prend en paramètre un graphe, le sommet de départ et le sommet de fin.
- Le constructeur initialise ces paramètres comme attribut.
Question 3 - Écrire une méthode initialisation. Cette méthode permet d'initialiser un dictionnaire.
- Les clés sont les différents sommets du graphe.
- Les valeurs sont des tableaux composés de 3 éléments :
- Une pondération, évaluée à l'infinie par défaut. On utilisera
float('Inf') - Un sommet, évalué à la chaine de caractère vide par défaut.
- Un booléen, évalue à
Falsepar défaut. Il indique si le sommet a été traité.
- Une pondération, évaluée à l'infinie par défaut. On utilisera
Seul le sommet de départ sera défini, avec une pondération à 0 et True pour le booléen.
def initialisation(self) -> dict :
pass
Voici le résultat attendu de cette méthode.
{'A': [0, 'A', True], 'B': [inf, '', False], 'C': [inf, '', False], 'D': [inf, '', False], 'E': [inf, '', False], 'F': [inf, '', False]}
Question 4 - Écrire une méthode mini. Cette méthode prend en paramètre un dictionnaire, du même format issu de la méthode initialisation. Elle retourne un tuple compose de la plus petite pondération et du sommet associé comme clé.
On choisira la plus petite valeur parmis les sommets non-traités.
def mini(self, dico) -> tuple:
pass
Voici un exemple avec le dictionnaire obtenu à la question précédente :
>>> d = self.initialisation()
{'A': [0, 'A', True], 'B': [inf, '', False], 'C': [inf, '', False], 'D': [inf, '', False], 'E': [inf, '', False], 'F': [inf, '', False]}
>>> mini = self.mini(d)
(inf, '', 'F') ou (inf, '', 'B')
Question 5 - Écrire la méthode run. Cette méthode implémente l'algorithme de Dijkstra. Elle pourra faire appel aux fonctions précédentes. Elle retourne une liste composée des différents sommets du graphe dans l'ordre du chemin.
def run(self) -> list :
pass