
¶ Exercice 1 - Parcours en largeur
Dans cet exercice, on souhaite implémenter l’algorithme du parcours en largeur en langage python en utilisant la programmation orientée objet. On l'appelle également parcours concentrique et il sert notamment à la recherche des plus courts chemins dans un graphe.
Pour cela, vous aurez besoin de plusieurs fichiers :
- La classe
Graphecréée dans le TP précédant. - La classe
Filecréée plus tôt dans l’année.
Question 1 - Dans un fichier main.py, écrire un programme permettant de construire le graphe ci-dessous.
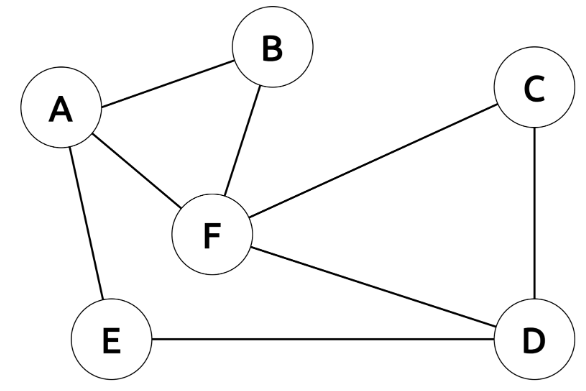
Question 2 - Dans la classe Graphe, écrire la méthode parcours_en_largeur qui prend en paramètre le sommet de départ. Cette méthode parcours le graphe à l'aide d'un parcours en largeur.
- Il faudra utiliser une file.
def parcours_en_largeur(self, depart) -> None:
'''
:param depart: (str)(int) Identifiant du sommet
:return: None
'''
Il n'existe pas obligatoirement un unique parcours en largeur. Néanmoins, la façon dont nous avons implémenté ce parcours donnera toujours le même résultat.
Question 3 - Essayer votre méthode sur le graphe créé à la question 1.
¶ Exercice 2 - Parcours en profondeur
Dans cet exercice, on souhaite implémenter l’algorithme du parcours en profondeur en langage python en utilisant la programmation orientée objet. Une application de ce type de parcours est la création de labyrinthes.
Pour cela, vous aurez besoin de plusieurs fichiers :
- La classe
Graphecréée dans le TP précédant. - La classe
Pilecréée plus tôt dans l’année.
Question 1 - Dans la classe Graphe, écrire la méthode parcours_en_profondeur qui prend en paramètre le sommet de départ. Cette méthode parcours le graphe à l'aide d'un parcours en profondeur.
def parcours_en_profondeur(self, depart) -> None:
'''
:param depart: (str)(int) Identifiant du sommet
:return: None
'''
Il n'existe pas obligatoirement un unique parcours en profondeur. Néanmoins, la façon dont nous avons implémenté ce parcours donnera toujours le même résultat.
Question 2 - Essayer votre méthode sur le graphe créé à l'exercice 1.
Question 3 - Écrire la méthode parcours_profondeur_recursif qui prend en paramètre le sommet de départ et une liste de sommet déjà parcourus, dont la valeur par défaut est une liste vide.
Cette méthode permet de parcourir un graphe en profondeur de manière récursive.
def parcours_profondeur_recursif(self, depart, deja_vu=[]) -> None:
'''
:param depart: (str)(int) Identifiant du sommet
:return: None
'''
¶ Exercice 3 - Recherche d'un chemin entre deux sommets
Dans cet exercice, on intéresse à l’algorithme permettant de rechercher un chemin (ou chaine) dans un graphe. Prenons comme exemple le graphe ci-dessous.
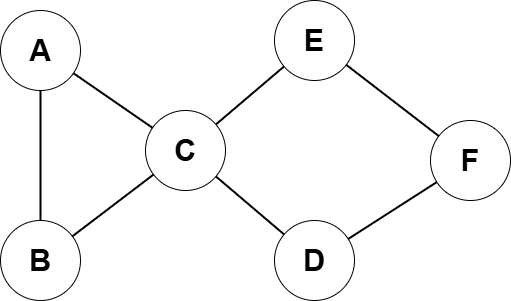
Voici le code pour créer le graphe de gauche :
g = Graphe(False)
sommets = ["A","B","C","D","E","F"]
for s in sommets:
g.ajouter_sommet(s)
g.ajouter_arete('A', 'B')
g.ajouter_arete('A', 'C')
g.ajouter_arete('B', 'C')
g.ajouter_arete('C', 'D')
g.ajouter_arete('C', 'E')
g.ajouter_arete('D', 'F')
g.ajouter_arete('E', 'F')
¶ Étape 1 : Construction du dictionnaire des parents
Pour trouver un chemin dans un graphe, la première étape consiste à parcourir ce graphe et de sauvegarder le parent de chaque sommet visité. En effet, il est essentiel de sauvegarder le parent du sommet visité afin de reconstruire le chemin une fois arrivé à destination.
Pour cela, on utilisera un dictionnaire dont la clé sera un sommet et la valeur sera le sommet parent lors du parcours. Par défaut, le parent du sommet de départ sera None.
Question 1 - Écrire une méthode dico_parent. Cette méthode prend en paramètre un sommet de départ. Elle parcourt le graphe en largeur et retourne le dictionnaire de parents.
def dico_parents(self, depart):
'''
:param depart: (str)(int) Identifiant du sommet
:return: (dict) Le dictionnaire de parent {sommet:parent}
'''
Voici un exemple du fonctionnement de cette fonction sur le graphe 1.
>>> dico = graphe.dico_parent('A')
>>> dico
{'A': None, 'B': 'A', 'C': 'A', 'D': 'C', 'E': 'C', 'F': 'D'}
¶ Étape 2 : Construction du chemin
L’étape 2 consiste à utiliser le dictionnaire de parents afin de reconstruire le chemin entre les 2 sommets. L’idée est de parcourir ce dictionnaire en partant du sommet d’arrivée. On remonte le chemin en regardant le parent de chaque sommet jusqu'à arriver au sommet de départ où son parent est égal à None.
Ci-dessous un exemple avec le dictionnaire des parents issus du graphe 1.
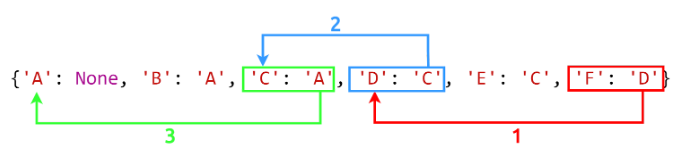
-
En partant du sommet F et en remontant les parents jusqu’au sommet de départ, on obtient le chemin suivant :
F - D - C - A. -
Pour obtenir le chemin final entre le sommet A et F, il suffit d’inverser cette liste de sommet et l’on obtient :
A - C - D - F.
Question 2 - Écrire une méthode chemin. Cette méthode prend en paramètre le sommet de départ et de sommet d’arrivée. Elle retourne une liste de sommets indiquant le chemin entre ces deux sommets.
Si aucun chemin n’existe entre ces deux sommets, la méthode retourne None.
def chemin(self, depart, arrive):
'''
:param depart: (str)(int) Identifiant du sommet de depart
:parem arrive: (str)(int) Identifiant du sommet d'arrive
:return: (list) La liste de sommets représentant un chemin
>>> graphe.chemin('A', 'F')
['A', 'C', 'D', 'F']
'''
Question 3 - Tester votre fonction avec les données suivantes :
| Graphe | Départ | Arrivée |
|---|---|---|
| Graphe 1 | A | F |
| Graphe 2 | B | C |
| Graphe 2 | C | F |
Cet algorithme permet de trouver le plus court chemin dans un graphe non-pondéré.
Il est notemment utilisé dans le protocole de routage
RIP.
¶ Exercice 4 - Le labyrinthe
L’objectif de cet exercice est de trouver un chemin permettant de sortir d’un labyrinthe. Pour cela, nous allons utiliser les algorithmes de parcours de graphes pour résoudre ce problème.
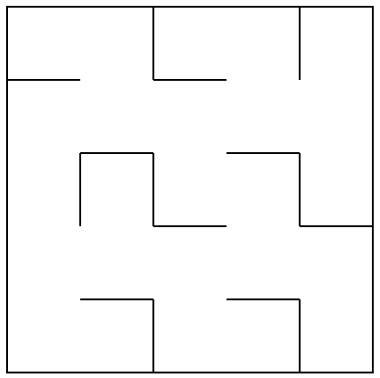
Considérons le labyrinthe ci-dessous :
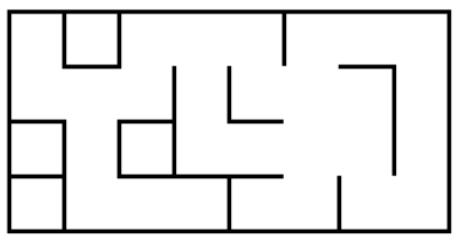
Ce labyrinthe se décompose en 4 lignes et 8 colonnes, soit 32 cases possibles. Pour représenter ce labyrinthe à l’aide d’un graphe, on décidera que :
- Chaque case du labyrinthe est représentée par un sommet du graphe
- Une arête est ajoutée entre 2 sommets quand le passage entre les 2 cases est possible.
Chaque sommet sera identifié par ses coordonnées x et y.
On obtient alors le graphe suivant :

Les arêtes relient les cases voisines quand le passage est possible. Si une paroi empêche de passer, on ne met pas d'arête. Par exemple, il n'y a pas d'arête entre les sommets (1,1) et (1,2) mais il y en a une entre (1,1) et (2,1).
Question 1 - Indiquer le calcul à faire pour obtenir l’ordre du graphe.
Question 2 - Indiquer si ce graphe est connexe.
Pour résoudre ce problème, nous allons utiliser la classe Graphe.
Question 3 - Créer un fichier main.py qui contiendra notre programme principal.
Question 4 - Créer une nouvelle instance de cette classe.
L’identifiant pour chaque sommet est le couple (x, y) représentant leurs coordonnées au sein du labyrinthe. Il faut donc créer les sommets (1,1), (1,2), (1,3)... jusqu'à (4,8).
Question 5 - Écrire un programme permettant d’ajouter les 32 sommets au graphe.
Pour ajouter toutes les arêtes, il n’a pas d’autre solution que de les ajouter une à une. Voici les lignes à écrire pour ajouter l’ensemble des arêtes au graphe.
laby.ajouter_arete((1,1),(2,1))
laby.ajouter_arete((2,1),(2,2))
laby.ajouter_arete((2,2),(2,3))
laby.ajouter_arete((2,2),(3,2))
laby.ajouter_arete((2,3),(1,3))
laby.ajouter_arete((1,3),(1,4))
laby.ajouter_arete((1,4),(1,5))
laby.ajouter_arete((1,4),(2,4))
laby.ajouter_arete((1,5),(2,5))
laby.ajouter_arete((2,7),(3,7))
laby.ajouter_arete((1,6),(1,7))
laby.ajouter_arete((2,4),(3,4))
laby.ajouter_arete((1,7),(1,8))
laby.ajouter_arete((1,8),(2,8))
laby.ajouter_arete((3,2),(4,2))
laby.ajouter_arete((4,2),(4,3))
laby.ajouter_arete((4,3),(4,4))
laby.ajouter_arete((3,4),(3,5))
laby.ajouter_arete((3,5),(3,6))
laby.ajouter_arete((3,6),(4,6))
laby.ajouter_arete((3,6),(3,7))
laby.ajouter_arete((4,6),(4,5))
laby.ajouter_arete((3,7),(4,7))
laby.ajouter_arete((4,7),(4,8))
laby.ajouter_arete((4,8),(3,8))
laby.ajouter_arete((2,8),(3,8))
laby.ajouter_arete((1,6),(2,6))
laby.ajouter_arete((2,5),(2,6))
laby.ajouter_arete((3,6),(2,6))
laby.ajouter_arete((2,7),(2,6))
Question 6 - Compléter votre programme, ajouter les lignes ci-dessus dans le fichier main.py.
¶ Parcourir le graphe
Il suffit maintenant d’utiliser l’algorithme de recherche d’un chemin dans un graphe pour déterminer un chemin possible permettant de sortir du labyrinthe.
La case de départ sera en (1,1) et la case d’arrivée sera (4,8).
Question 10 - Utiliser la méthode chemin pour trouver le chemin permettant de sortir du labyrinthe.
¶ Dessiner le chemin
Pour faciliter la compréhension du chemin, on peut le dessiner sur le labyrinthe à l’aide du module Turtle et d’un ensemble de fonctions déjà écrites.
Pour cela, il suffit de récupérer le module labyrinthe.py disponible ci-dessous.
Question 11 - Dans le fichier main.py, importer le module labyrinthe.py.
Question 12 - Utiliser la fonction dessiner_parcours pour afficher un dessin du chemin à prendre. Voici la documentation de la méthode .
def dessiner_parcours(laby, p, taille_cote, nb_ligne, nb_colonne):
'''
:param laby: (Graphe) Le graphe représentant le labyrinthe
:param p: (list) La liste des sommets à parcourir représentant un chemin
:param taille_cote: (int) La taille de case qui compose de labyrinthe. = 50
:param nb_ligne: (int) Nombre de lignes du labyrinthe
:param nb_colonne: (int) Nombre de colonnes du labyrinthe
'''
Vous devez voir le tracer pour sortir du labyrinthe !
Question 13 - Trouver et afficher une solution pour sortir du labyrinthe ci-dessous.
¶ Exercice 5 - Détecter la présence de cycle
Un cycle est un chemin (ou une chaine) dont le sommet de départ est le même que le sommet d’arrivée. Dans cette partie, nous allons nous intéresser à un algorithme permettant d’indiquer si un cycle est présent ou non dans un graphe orienté et non orienté.
Pour cela, nous allons considérer les deux graphes ci-dessous.
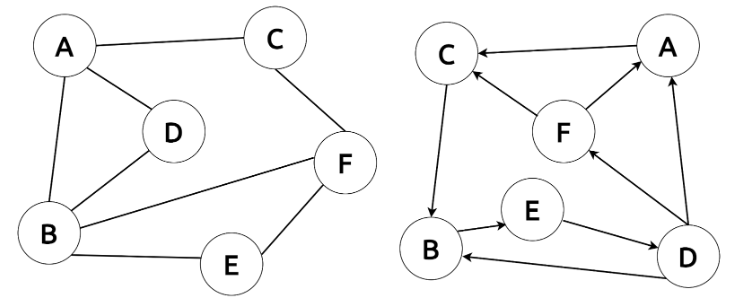
- Le graphe 1 contient un cycle, par exemple A - B - D - A
- Le graphe 2 contient un cycle, par exemple B - E - D - B
L’algorithme est assez simple et ressemble aux algorithmes de parcours. En effet, lorsqu’on regarde les voisins du sommet traité, il suffit de retourner True si ce voisin est déjà visité. On continue le traitement si le sommet n’est pas visité.
À la fin de la méthode, on retourne False si à aucun moment, on retombe sur un sommet déjà visité.
Question 1 - Écrire la méthode possede_cycle. Cette méthode prend en paramètre le sommet de départ. Elle retourne True si le graphe possède un cycle, False sinon. Voici le fonctionnement général de l'alogitihme :
- Empilez le sommet de départ.
- Dépilez la pile et récupérer un sommet.
- Si ce sommet n'est pas encore visité :
- Ajouter ce sommet à la liste des sommets visités.
- Ajoutez les voisins non visités à la pile.
- Vérifiez si un voisin déjà visité n'est pas le parentd direct → cycle.
- Retournez True si un cycle est trouvé, sinon False.
def possede_cycle(self, depart) -> bool :
'''
:param depart: (str)(int) Identifiant du sommet
:return: (bool) Vrai si le graphe possede un cycle, False sinon
>>> graphe1.possede_un_cycle("B")
False
>>> graphe2.possede_un_cycle("A")
True
'''
Question 2 - Essayer votre méthode sur les deux graphes ci-dessus.