
¶ Exercice 1 - Recherche d’un élément dans une liste non triée
L’objectif de cet exercice est d’écrire plusieurs fonctions permettant d’indiquer la présence ou non d’un élément dans une liste non triée.
Ci-dessous la liste à utiliser pour tester vos fonctions :
tab = [5, 0, 3, 9, 4, 6, 7, 8]
¶ Méthode 1 - La recherche naïve
Dans cette première partie, nous allons nous concentrer sur la recherche dite « naïve ». Cette fonction parcourt les éléments du tableau de manière séquentielle.
Question 1 - Écrire la fonction recherche_naive. Cette fonction prend en paramètre une liste d'entiers et un entier. Elle retourne True si l'élément est présent dans la liste, False sinon.
def recherche_naive(liste_entiers:list, x:int) -> bool :
pass
¶ Méthode 2 - La recherche « diviser pour régner »
L'idée de la méthode « diviser pour régner » est de diviser la liste de recherche à chaque appel récursif. À la fin de tous ces appel, on obtient des listes de taille 1. Il suffit alors de les comparer et de combiner les booléens obtenus via l’opérateur logique or.
La condition d’arrêt de la récursivité est obtenue lorsqu’une liste possède un seul élément, car il est alors facile de déterminer si l’élément recherché appartient à cette liste.
Voici les 3 étapes de cette fonction :
- Diviser la liste en deux parties.
- Rechercher la présence de l’élément dans chaque sous-liste de taille 1
- Effectuer les appels récursifs si les tailles des listes sont supérieures à 1.
- Combiner le résultat des deux parties avec l’opérateur
or.
Question 2 - Écrire la fonction recherche_dpr. Cette fonction prend en paramètre une liste d'entiers et un entier. Elle retourne True si l'élément est présent dans la liste, False sinon. Elle utilise la méthode « diviser pour régner ».
def recherche_dpr(liste_entiers:list, x:int) -> bool :
pass
¶ Comparaison des deux méthodes
Pour évaluer la performance des deux fonctions, nous allons utiliser le module timeit qui permet de mesurer le temps d'exécution des deux fonctions sur des listes de taille aléatoire.
Le code ci-dessous effectue des milliers d'essaie de ces deux fonctions avec des tableaux de taille croissante. Le temps d'exécution de chaque appel de fonction est ajouté dans une liste, qui est utilisée pour dessiner un graphique à l'aide du module pyplot.
Dans ce cas, on essaye de trouver la valeur -1, qui est le pire des cas, car les tableaux ne contiennt que des nombres positifs.
Question 3 - Vérifier la bonne installation du module matplotlib et importer le module dans votre programme à l'aide de l'instruction import matplotlib.pyplot as plt.
Question 4 - Copier/coller le ci-dessous pour voir la comparaison entre les deux méthodes.
x1 = [x for x in range(10000,50000, 100)]
y1 = []
y2 = []
for i in x1:
t = [random.randint(0,1000) for _ in range(i)]
y1.append(timeit.timeit(setup="from __main__ import recherche_naive, t",stmt='recherche_naive(t,-1)',number=1))
y2.append(timeit.timeit(setup="from __main__ import recherche_dpr, t",stmt='recherche_dpr(t,-1)',number=1))
plt.plot(x1, y1, label="Recherche naive")
plt.plot(x1, y2, label="Recherche dpr")
plt.xlabel("Taille des listes")
plt.ylabel("Temps d'exécution")
plt.legend()
plt.show()
Les fonctions ont un coût linéaire, mais la méthode naïve semble être la plus efficace !
Dans cette situation, la liste n'est pas triée. La méthode « diviser pour régner » est plus efficace si l'on travaille avec une structure de donnée particulière, comme une liste triée.
¶ Exercice 2 - Recherche d’un élément dans une liste triée
Cette fois, on s'intéresse à la recherche d'un élément dans une liste triée selon la méthode de la dichotomie.
Ci-dessous la liste à utiliser pour tester vos fonctions :
tab = [-1, 0, 3, 5, 6, 8, 10, 14, 17, 19, 27]
¶ Méthode 1 - La dichotomie naïve
Question 1 - Écrire la fonction dicho_naive. Cette fonction prend en paramètre une liste d'entiers et un entier. Elle retourne True si l'élément est présent dans la liste, False sinon. Elle utilise le principe de la dichotomie vu en classe de première.
def dicho_naive(liste_entiers:list, x:int) -> bool :
pass
¶ Méthode 2 - La dichotomie « diviser pour régner »
Voici les étapes permettant d’écrire cette fonction en utilisant la méthode « diviser pour régner » :
- Diviser la liste en deux sous-listes.
- Rechercher la présence de l’élément dans chaque sous-liste de taille 1
- Effectuer les appels récursifs si les tailles des listes sont supérieures à 1. On utilisera uniquement la « bonne » des deux sous-listes.
- Ici, pas de phase « combiner » car on ne « travaille » que sur l’une des deux sous-listes.
Question 2 - Écrire la fonction dicho_dpr. Cette fonction prend en paramètre une liste d'entiers et un entier. Elle retourne True si l'élément est présent dans la liste, False sinon. Elle utilise le principe de la dichotomie et de la méthode « diviser pour régner ».
def dicho_dpr(liste_entiers:list, x:int) -> bool :
pass
¶ Méthode 3 - Comparaison des 3 méthodes
Pour voir le gain de performance, nous allons comparer 3 méthodes :
- La recherche naïve de l'exercice précédent.
- La recherche dichotomique naïve.
- La recherche dichotomique « diviser pour régner ».
Question 3 - À l'aide du programme de la question 1, générer un graphique permettant de comparer les 3 méthodes de recherche.
Dans ce cas, il faudra utiliser un tableau trié en changeant la ligne suivante :
t = sorted([random.randint(0,i) for _ in range(i)])
Vous devez obtenir un graphique proche de celui-ci.
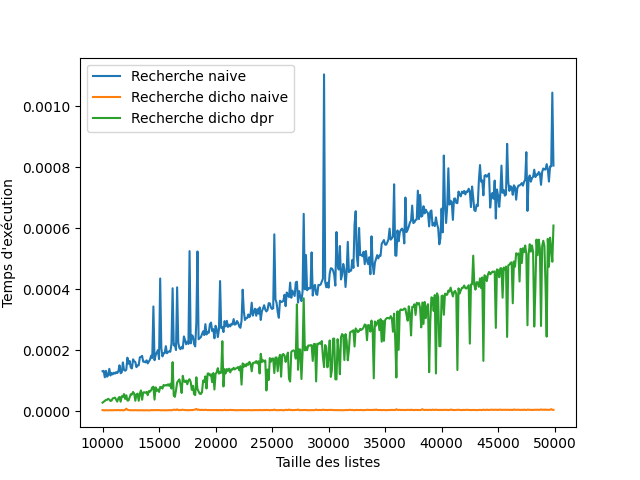
La méthode diviser pour régner est moins efficace que la méthode classique de la dichotomie. Cela peut s'expliquer car Python n’est pas un langage fonctionnel, les récursions ne sont pas optimisées et prennent plus de temps.
¶ Exercice 3 - Le tri fusion
Le tri fusion est un algorithme de tri utilisant la méthode « diviser pour régner ». Il consiste à trier récursivement 2 sous-listes, puis à combiner ses listes triées pour en former qu’une seule.
On peut représenter le principe du tri fusion avec le schéma ci-dessous :
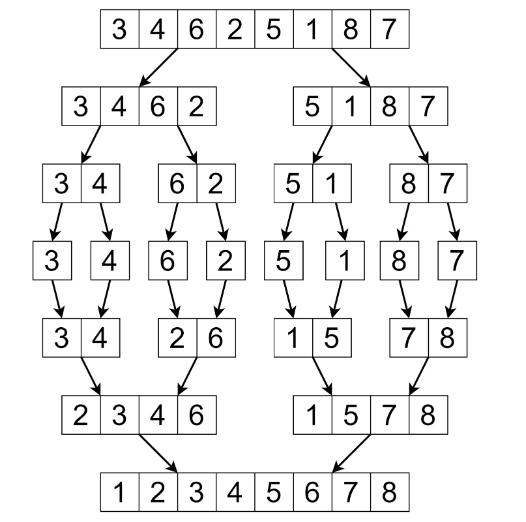
Voici donc les trois étapes de cet algorithme :
- Diviser la liste en deux sous-listes de même taille (à un élément près)
- Trier récursivement chacune de ces deux sous-listes. Arrêter la récursion lorsque les listes n’ont plus qu’un seul élément.
- Fusionner les deux sous-listes triées en une seule.
Question 1 - Écrire la fonction récursivefusion. Cette fonction prend en paramètre 2 listes et fusionne ces deux listes en une seule liste triée.
def fusion(l1:list, l2:list) -> list :
pass
Question 2 - Écrire la fonction récursive tri_fusion. Cette fonction prend en paramètre une liste et retourne cette même liste triée. Elle utilise la méthode « diviser pour régner ».
def tri_fusion(l:list) -> list :
pass
¶ Efficacité du tri fusion
Pour observer la réelle efficacité du tri fusion, nous allons le comparer avec 2 autres découverts en première : le tri par sélection et le tri par insertion.
Voici le code des deux tris :
def tri_selection(liste):
n = len(liste)
for i in range(n):
min = i
for j in range(i+1, n):
if liste[j] < liste[min]:
min = j
liste[i], liste[min] = liste[min], liste[i]
return liste
def tri_par_insertion(liste):
n = len(liste)
for i in range(1, n):
valeur_a_inserer = liste[i]
j = i - 1
# Décale les éléments plus grands vers la droite
while j >= 0 and liste[j] > valeur_a_inserer:
liste[j + 1] = liste[j]
j -= 1
# Insère la valeur à la bonne position
liste[j + 1] = valeur_a_inserer
Comme dans l'exercice 1, nous allons analyser le temps d'exécution de chacun des tris sur plusieurs listes de taille entre 1 et 1000 éléments. Chaque liste sera composés d'entiers choisi aléatoirement en 0 et 500
Les temps d'exécution obtenus pour chaque tri seront ajoutés dans une liste afin d'y générer un graphique.
Question 3 - Générer le graphique permettant d'observer l'efficacité des 3 tris.
Vous devez obetenir un graphe proche de celui-ci.
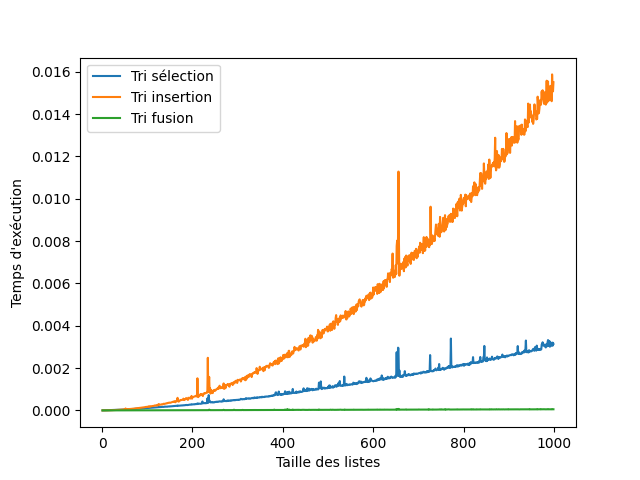
¶ Calcul de la complexité du tri fusion
Pour trouver la complexité du tri fusion, on va s'intéresser au coût des étapes de divisions et de fusion :
- À chaque appel récusif, la taille de la liste est divisée par 2. Le nombre de divisions nécessaires pour arriver à des morceaux de taille 1 est .
- Lors de la phase de fusion, on compare et fusionne les éléments deux à deux. À chaque niveau récursif, chaque élément du tableau est impliqué dans une opération de fusion. Donc à chaque niveau, on a opérations de fusion.
En résumé, la complexité totale du tri fusion est de l'ordre de que l'on peut écrire .
¶ Exercice 4 - Recherche le maximum dans une liste
Dans cet exercice, nous nous intéresserons à la recherche du nombre maximum au sein d’une liste de nombre.
En utilisant la méthode « diviser pour régner », l’idée est de rechercher le maximum dans la première moitié de la liste et dans la seconde moitié de la liste. Puis de rediviser ces listes jusqu'à obtenir des listes de taille 1.
Voici les trois étapes de la fonction :
- Diviser la liste en deux sous-listes
- Rechercher récursivement le maximum de chacune de ces sous-listes.
- Retourner le plus grand des deux maximums précédents.
Question 1 - Écrire la fonction récursive maximum. Cette fonction prend en paramètre une liste et retourne la plus grande valeur de cette liste. Elle utilise la méthode « diviser pour régner ».
def maximum(l:list) -> list :
pass
¶ Exercice 5 - Algorithme d’exponentiation rapide
¶ Algorithme naïf
On souhaite calculer . La méthode basique serait d’écrire une fonction qui multiplie le nombre 76 fois par lui-même.
Question 1 - Écrire la fonction puissance_naive. Cette fonction prend en paramètre deux entiers x et n. Elle retourne le résultat de x puissance n.
- Pour avoir des résultats pertinents, nous allons utiliser une boucle pour construire cette fonction.
def puissance_naive(x:int, n:int) -> int :
pass
¶ Algorithme « Diviser pour régner »
La version naïve n’est pas très rapide. En effet, pour , il faut réaliser 76 opérations !
L’idée est alors d’utiliser la méthode « diviser pour régner ». On va donc diviser le problème en deux et effectuer le calcul suivant : , ce qui revient à calculer .
On obtient maintenant seulement 39 opérations :
- 38 multiplications pour calculer .
- 1 multiplication pour faire le carré du résultat.
On peut continuer : (5^{38})^{2} = ((5^{19})^{2})^
Dans ce cas, on obtient 21 opérations :
- 19 multiplications.
- 2 multiplications pour faire les 2 mises au carré du résultat.
Alors que l'algorithme naïf demande de l'ordre de multiplications pour calculer , l'algorithme d'exponentiation rapide est de l'ordre de multiplications.
Question 2 - Écrire la fonction puissance_dpr. Cette fonction prend en paramètre deux entiers x et n. Elle retourne le résultat de x puissance n en utilisant la méthode « diviser pour régner ».
def puissance_dpr(x:int, n:int) -> int :
pass
¶ Efficacité
Pour comparer l'efficacité de la méthode, voici un programme permettant de calculer 1000 fois le calcul et de mesurer le temps d'exécution.
x1 = timeit.timeit(setup="from __main__ import puissance_naive",stmt='puissance_naive(589,7601)',number=1000)
x2 = timeit.timeit(setup="from __main__ import puissance_dpr",stmt='puissance_dpr(589,7601)',number=1000)
print("Methode classique :", x1, "secondes")
print("Methode diviser pour régner :", x2, "secondes")
Question 3 - Essayer le programme précédent afin d'observer le gain de temps d'exécution.