
¶ Exercice 1 - Évaluation d'une expression arithmétique
Une expression arithmétique ne comportant que les 4 opérations +, -, x et / peut être représentée sous la forme d'un arbre binaire. Les noeuds internes sont des opérateurs et les feuilles sont des nombres.
Dans un tel arbre, la disposition des noeuds dans l'arbre joue le rôle des parenthèses.
Voici un exemple avec l'arbre ci-dessous. Il représente l'expression 3 x (8 + 7) - (2 + 1)
.png)
Question 1 - Dans un nouveau fichier ArbreArithmetique.py, créer une nouvelle classe ArbreArithmetique qui hérite de la classe Arbre.
class ArbreArithmetique (Arbre):
def __init__(self, noeud, gauche=None, droite=None):
super().__init__(noeud, gauche, droite)
La notion d'héritage n'est pas au programme de terminale NSI, mais permet de simplifier énormément la création d'une nouvelle classe basée sur une autre.
Question 2 - Dans un fichier main.py, écrire le programme permettant de construire l'arbre arithmétique ci-dessus.
Question 3 - Utiliser les 3 algorithmes de parcours en profondeur sur l'arbre de la question 2.
- Parcours préfixe
- Parcours infixe.
- Parcours postfixe.
Question 3 - Dans la classe ArbreArithmetique, écrire une nouvelle méthode récursive evaluer qui renvoie le résultat de l'expression représentée sous la forme d'un arbre.
¶ Exercice 2 - Codage de Huffman
Dans cet exercice, on s'intéresse à une méthode de compression de données inventée par David Albert HUFFMAN en 1952.
Cette méthode permet de réduire la longueur du codage d’un texte (entre autres). La compression se fait en codant les caractères les plus fréquents par des codes courts et les caractères les moins fréquents par des codes longs.
On observe ainsi des réductions de taille de fichier de l’ordre de 20 à 90%. C’est une méthode de compression largement utilisée, souvent en complément d’autres algorithmes.
Pour la suite de cet exercice, on considère que notre alphabet est composé de seulement 8 lettres : A B C D E F G H.
¶ Partie 1 - Découverte du codage
Le début de cet exercice est à faire sur la feuille d'activité.
¶ Partie 2 - Implémentation de l'algorithme de Huffman
Pour cette partie, vous aurez besoin de la classe Arbre.
¶ Génération de l'arbre de Huffman
Question 1 - Créer un fichier nommé Huffman.py.
Question 2 - Écrire une fonction dico_occurence qui prend en paramètre une chaine de caractères représentant le texte à coder. Cette fonction retourne un dictionnaire dont les clés sont les différents caractères du texte et les valeurs le nombre d'occurrences de la lettre.
def dico_occurence(texte:str) -> dict :
pass
Question 3 - Écrire une fonction generer_arbre_huffman qui prend en paramètre le dictionnaire d'occurrences. Cette fonction retourne un objet Arbre qui correspond à un arbre de Huffman associé au dictionnaire d'occurrences.
def generer_arbre_huffman(dico_occurence:dict) -> Arbre:
pass
Voici un rappel de l'algorithme :
- Créer une liste d'arbre (sans fils) dont chaque noeud est composé d'un caractère du texte et de son occurrence sous la forme d'un tuple.
- Retirer de la liste les 2 arbres ayant les nombres d’occurrence les plus faibles.
- Générer nouvel arbre dont les fils gauche et droit sont les 2 arbres retirés de la liste. La valeur du nœud sera un tuple composé d’une chaine de caractères vide et de la somme des occurrences des 2 fils.
- On ajoute le nouvel arbre dans la liste.
- On recommence l’étape 2.
Vous pouvez créer une fonction annexe
enlever_miniqui enlève et retourne l'arbre avec la plus petite occurence parmi la liste d'arbre.
def enlever_mini(liste:list) -> Arbre:
pass
¶ Codage du texte
On s'intéresse ici au codage des textes. Dans un premier temps, nous allons générer un dictionnaire qui associe chaque caractère à son code dans l'arbre de Huffman. Par exemple : d = {'a':00, 'e':01}
Question 4 - Écrire la fonction récursive generer_dico_huffman dont la signature de la fonction est présentée ci-dessous.
- Cette fonction modifie par effet de bord le dictionnaire
dicopassé en paramètre. - Cette fonction est récursive : le paramètre
cheminest vide par défaut, mais évoluera au fur et mesure des appels récursifs. On rappelle que :- Le chemin passant par le fils gauche est associé au symbole « 0 »
- Le chemin passant par le fils droit est associé au symbole « 1 »
def generer_dico_huffman(arbre:Arbre, dico:dict, chemin:str="") -> None:
pass
Question 5 - Écrire une fonction codage_huffman qui prend en paramètre une chaine de caractères et son arbre de Huffman associé. Cette fonction renvoie le code de la chaine de caractères selon le codage de Huffman.
>>> codage_huffman("BADGE")
"001 000 11 10 01"
Question 6 - Écrire une fonction decodage_huffman qui prend en paramètre une chaine de caractères. Cette fonction décode la chaine de caractère et renvoie le texte en clair.
¶ Exercice 3 - Le morse
Même si le morse est un langage binaire un peu démodé, il peut être intéressant de se pencher sur la possibilité d'un décodage rapide de tel message pour voir l’intérêt des arbres binaires.
¶ Arbre morse
Il est possible de représenter chaque lettre de l'alphabet dans un arbre morse. Dans cet arbre, on considère seulement les lettres de A à Z, les chiffre de 1 à 9 et le symbole /.
On rappelle que le code Morse est constitué de points et de tirets :
- La lettre « S » est représentée par 3 points "=
... - La lettre « O » est représentée par trois tirets
---.
On considère que les points sont représentés par le fils gauche d'un noeud et un tiret par le fils droit d'un noeud. Voici la représentation graphique d'un arbre contenant l'alphabet :
- Le symbole
*indique qu'on ne prend pas en compte ce caractère.
¶ Génération de l'arbre morse
Dans cette partie, on s'intéresse à la génération de l'arbre morse. L'une des méthodes pour générer cet arbre consiste à utiliser un dictionnaire.
Question 1 - Écrire une fonction creer_arbre_morse. Cette fonction renvoie un arbre binaire représentant le schéma ci-dessous. Il permet de construire un arbre morse.
def creer_arbre_morse():
dicomorse = {'A':'.-' , 'B':'-...','C':'-.-.', 'D':'-..', 'E':'.','F':'..-.', 'G':'--.', 'H':'....','I':'..','J':'.---','K':'-.-','L':'.-..', 'M':'--', 'N':'-.','O':'---', 'P':'.--.', 'Q':'--.-','R':'.-.', 'S':'...','T':'-','U':'..-', 'V':'...-', 'W':'.--','X':'-..-', 'Y':'-.--', 'Z':'--..','1':'.----', '2':'..---', '3':'...--','4':'....-', '5':'.....', '6':'-....','7':'--...', '8':'---..', '9':'----.','0':'-----', '/':'-..-.'}
pass
¶ La fonction de décodage
Question 2 - Écrire une fonction decoder_morse qui prend en paramètre une chaine de caractères représentant un message en morse et un arbre binaire morse. Cette fonction retourne une chaine de caractères représentant la traduction du message morse.
def decoder_morse(code:str, arbre_morse:Arbre) -> str:
pass
Le message morse
... --- ...signifieSOS.
¶ La fonction de codage
La première étape consiste à construire un dictionnaire qui associe chaque caractère à son code Morse en parcourant l'arbre Morse.
Question 3 - Écrire une fonction generer_dico_morse qui prend en paramètre un arbre morse, un dictionnaire vide et une chaine de caractères, par défaut vide, qui permettra de sauvegarder le chemin au fur et à mesure des appels récursifs.
Cette fonction complète le dictionnaire par effet de bord, en ajoutant une association entre un caractère et le chemin effectué pour trouver le caractère dans l'arbre.
def generer_dico_morse(arbre:Arbre, dico:dict, chemin:str="") -> None:
"""
Fonction récursive pour générer un dictionnaire de codage Morse.
:param arbre: Arbre Morse.
:param dico: Dictionnaire à remplir (effet de bord).
:param chemin: Code Morse actuel, qui évolue récursivement.
"""
Question 4 - Écrire une fonction coder_morse qui prend en paramètre une chaine de caractères représentant un message et un arbre binaire morse. Cette fonction retourne une chaine de caractères représentant le code morse du message.
- Il faut créer le dictionnaire morse en utilisant la fonction de la question précédente.
def coder_morse(text:str, arbre_morse:Arbre) -> str:
pass
¶ Exercice 4 - Arbre d'arité non borné
Tous les arbres ne sont pas binaires. Par exemple, si on souhaite représenter une arborescence de fichiers, il n’est pas possible d'utiliser les arbres binaires.
On préfèrera utiliser des arbres d’arité non bornée, c’est-à-dire où chaque nœud a une étiquette et ainsi qu’une liste d’enfants qui sont eux-mêmes des arbres.
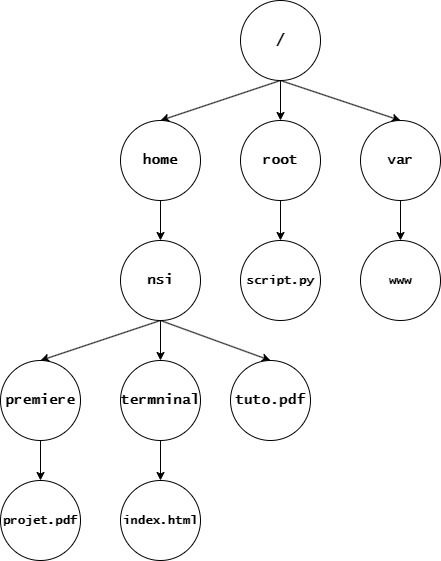
Question 1 - Dans un fichier Noeud.py, écrire une classe Noeud. Cette classe permettra de représenter un noeud dans une arborescence de fichier.
La classe aura 2 attributs :
- Un nom, qui correspond au nom du noeud dans l'arborescence.
- Une liste de noeud enfants, qui correspond à des sous-dossiers dans l'arborescence.
Question 2 - Écrire deux classes Fichier et Repertoire. Ces deux classes héritent de la classe Noeud.
On ajoutera les méthodes est_fichier et est_repertoire dans ces deux classes. Ces méthodes retournent un booléen permettant de distinguer les répertoires des autres fichiers.
Question 3 - Dans un fichier main.py, écrire un programme permettant de représenter l'arborescence de fichier ci-dessus.
Question 4 - On veut désormais simuler l’affichage récursif de l’ensemble des fichiers d’un répertoire donné, tel qu’on l’obtient sous Unix en tapant la commande bash ls -R. Sur l’arborescence donnée en exemple précédemment, on veut obtenir:
souris.jpg Users Applications System
home/Users:
bmonmege jdupont
home/Users/bmonmege:
Documents Downloads
home/Users/bmonmege/Documents:
présentation.ppt texte.txt
home/Users/bmonmege/Downloads:
chaton.jpg
home/Users/jdupont:
Documents
home/Users/jdupont/Documents:
home/Applications:
Firefox
home/System:
Dans la classe Noeud, écrire la méthode ls. Cette méthode simule le fonctionnement de la commande bash ls -R.
- Cette commande affiche le contenu de chaque dossier de manière récursive.
- Cet affichage correspond à un parcours préfixe de l’arborescence.