
¶ Exercice 1 - Une classe ABR
Question 1 - Dans un nouveau fichier ABR.py, créer une nouvelle classe ABR qui hérite de la classe Arbre.
class ABR (Arbre):
def __init__(self, noeud, gauche=None, droite=None):
super().__init__(noeud, gauche, droite)
La notion d'héritage n'est pas au programme de terminale NSI, mais permet de simplifier énormément la création d'une nouvelle classe basée sur une autre.
Question 2 - Dans un fichier main.py, écrire le programme permettant de construire l'ABR suivant.

Si vous utilisez la méthode
insererde la classeArbre, cela ne fonctionnera pas. En effet, elle ajoute, en tant que fils, des instances de la classeArbreet non de la classeABR.Pour l'utiliser, il faudra réécrire la méthode
insererdans la classeABR.
Question 3 - Dans la classe ABR, écrire une méthode est_ABR_recursive. Cette méthode renvoie True si l'arbre courant est un ABR, False sinon.
- On utilisera une méthode récursive
def est_ABR_recursive(self) -> bool :
return
Question 4 - Écrire une méthode privée __construire_liste_infixe. Cette méthode prend en paramètre une liste vide par défaut. Cette méthode effectue un parcours en profondeur infixe et ajoute les noeuds de l'arbre dans la liste.
- Cette méthode génère un effet de bord et ne renvoie rien.
def __construire_liste_infixe(self, l=[]):
return
Les méthodes privées sont des méthodes qui ne peuvent pas être utilisées à l'extérieur de la classe. En python, leur nom est précédé du symbole
__.
Question 5 - Dans la classe ABR, écrire une méthode est_ABR_infixe. Cette méthode faire appel à la méthode __construire_liste_infixe afin de générer une liste. Elle renvoie True si l'arbre courant est un ABR, False sinon.
def est_ABR_infixe(self) -> bool :
return
Question 6 - Écrire une méthode insertion. Cette méthode prend en paramètre une valeur et l'insère dans l'arbre selon les propriétés d'un arbre binaire.
def insertion(self, valeur) -> None:
return
Question 6 - Dans un fichier main.py, écrire le programme permettant d'ajouter les valeurs 10 et 1 dans l'arbre binaire de recherche.
Question 7 - Écrire une méthode insertion_liste. Cette méthode prend en paramètre une liste de valeurs et les ajoute dans un arbre selon les propriétés d'un arbre binaire.
def insertion_liste(self, liste) -> None:
return
Question 7 - Dans un fichier main.py, écrire le programme permettant d'ajouter la liste de valeurs suivante dans un ABR : [15, 5, 18, -4, 12, 3, 20, 14, 36, -9, 3, 8, 50]
¶ Exercice 2 - Rechercher des éléments
Question 1 - Dans la classe ABR, écrire une méthode maxi. Cette méthode renvoie la valeur maximale d'un ABR.
def maxi(self) -> int :
return
Question 3- Dans la classe ABR, écrire une méthode mini. Cette méthode renvoie la valeur minimale d'un ABR.
def mini(self) -> int:
return
Question 4 - Dans le fichier main.py, générer 2 ABR à l'aide d'une liste de valeurs allant de 1 à 31.
- Le premier ABR sera un ABR le plus équilibré possible
- Le second ABR sera un ABR filiforme.
Pour vous aider à construire ses ABR, on utilisera la fonction insertion_liste qui permet d'ajouter plusieurs valeur dans un ABR.
- Il faut trouver le bon ordre des valeurs dans la liste pour créer ces arbres.
Question 5 - Utiliser les méthodes taille et hauteur sur les deux ABR pour vérifier :
- Que leurs tailles sont identiques (31 noeuds)
- Que leurs hauteurs sont différentes. (30 pour l'ABR filiforme, pour l'arbre équilibré)
Question 6 - Écrire la méthode rechercher. Cette méthode prend en paramètre une valeur et retourne True si cette valeur est présente dans l'ABR, False sinon.
def rechercher(self, v) -> bool:
return
Question 7 - Écrire la méthode rechercher_cout. Cette méthode est une version améliorée de la méthode précédente. En plus du booléen, elle retourne le nombre de comparaisons effectuées pour trouver la valeur.
def rechercher_cout(self, v, comparaison=0) -> tuple:
return
Question 8 - Essayer la méthode recherche_cout sur les 2 ABR générés à la question 4.
Le coût de la recherche dans un ABR équilibré doit être beaucoup plus faible que dans un ABR filiforme.
¶ Pour aller plus loin : équilibrage d'un ABR
Avec les exercices précédents, on remarque clairement qu’un arbre équilibré donne en moyenne de meilleurs résultats qu’un arbre filiforme ou dégénéré.
Cette notion d’arbre équilibré (balanced tree) n’est pas au programme de terminale, mais nous allons essayer de découvrir un algorithme permettant l'équilibrage d'un arbre binaire de recherche.
¶ Pourquoi équilibrer un arbre ?
Sur un ABR équilibré, la recherche d’un élément est en moyenne en log2(n), comme dans une recherche dichotomique dans une liste. On peut alors se poser la question de l’intérêt d’utiliser un ABR.
La réponse tient dans le temps mis pour ajouter ou supprimer un élément :
- Dans une liste, on est en (complexité linéaire),
- Dans un ABR, on est en (complexité logarithmique).
Il est donc important que notre ABR soit équilibré, et que les méthodes d'insertion et de suppressions conservent l'ordre des noeuds de ces ABR. Il existe plusieurs techniques permettant d'obtenir des ABR équilibrés :
- les arbres AVL ;
- les arbres rouge-noir ;
- les arbres 2-3 ;
- les arbres 2-3-4 ;
- les B-arbres.
¶ Les arbres AVL
En informatique, les arbres AVL ont été historiquement les premiers arbres binaires de recherche automatiquement équilibrés.
La dénomination « arbre AVL » provient des noms respectifs de ses deux inventeurs, respectivement Georgii Adelson-Velsky et Evguenii Landis, qui l'ont publié en 1962 sous le titre « An Algorithm for the Organization of Information ».
¶ Le principe
Dans un arbre AVL, pour tout nœud, les hauteurs des sous-arbres gauche et droit diffèrent au plus de 1 (avec, par convention, le fait que la hauteur d’un arbre vide est -1).
Lors d’une insertion dans un arbre AVL, on rééquilibre l’arbre grâce à un algorithme reposant sur 2 opérations appelées rotation gauche et rotation droite préservant les propriétés d’un arbre binaire de recherche.
¶ Les algorithmes de rotation
L'algorithme de la méthode de rotation_gauche est une opération utilisée sur un arbre binaire. Il s'agit de réorganiser les liens entre les nœuds pour réduire la hauteur du sous-arbre droit tout en conservant les propriétés d'un arbre binaire de recherche (ABR).
Sur le même principe, l'algorithme de la méthode de rotation_droite est utilisé pour réduire la hauteur du sous arbre gauche.
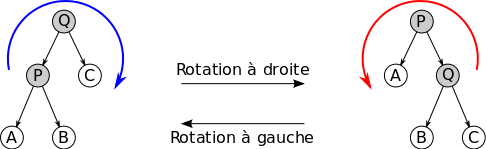
Sur ce schéma, une rotation à gauche ou à droite ne permet pas réduire la hauteur de l'arbre. C'est un enchainement précis de rotations à droite ou à gauche qui permettent d'équilibrer un ABR, selon l'algortihme présenté plus bas.
Pour mieux comprendre le principe général de l'algorithme, vous pouvez regarder cette vidéo qui montre le principe de l'équilibrage à chaque nouvelle insertion dans l'ABR.
¶ Explication de l'algorithme
La rotation gauche considère la racine d'un ABR et avec son sous-arbre droit (appelé pivot) et fait du pivot la nouvelle racine du sous-arbre. La racine d'origine devient le sous-arbre gauche du pivot.
Voici l'algorithme de la rotation gauche :
- Vérifiez qu'une rotation gauche est possible : il faut que le sous-arbre droit de la racine ne soit pas vide.
- Identifiez le pivot comme le sous-arbre droit de la racine.
- Attribuer au fils droit de la racine le fils gauche du pivot.
- Attribuer la racine comme fils gauche du pivot.
- Retourne le pivot (qui sera la nouvelle racine de notre arbre).
Question 1 - Dans la classe ABR, écrire la méthode rotation_gauche en vous aidant l'algorithme présenté ci-dessus. La méthode retourne l'ABR après une rotation gauche.
def rotation_gauche(self) -> ABR:
pass
Question 2 - Dans la classe ABR, écrire la méthode rotation_droite en vous aidant l'algorithme présenté ci-dessus. La méthode retourne l'ABR après une rotation droite.
def rotation_droite(self) -> ABR:
pass
Question 3 - Essayer les deux fonctions avec l'exemple suivant :
# TEST ROTATION
a = ABR(3)
a.insertion_liste([4,1,0,2])
a.affiche()
a =a.rotation_droite()
a.affiche()
a = a.rotation_gauche()
a.affiche()
¶ L'algorithme d'équilibrage
L'objectif est de maintenir l'équilibre de l'arbre binaire, où pour chaque nœud, la différence de hauteur entre son sous-arbre gauche et son sous-arbre droit ne dépasse pas 1. Si cette différence est plus grande, on applique des rotations pour rééquilibrer l'arbre.
¶ Les étapes
Lorsque la différence de hauteur entre le sous-arbre gauche et le sous-arbre droit d'un nœud est trop grande (c'est-à-dire plus grande que 1), on effectue des rotations pour rééquilibrer l'arbre. Ces cas sont classifiés en fonction de la direction dans laquelle le déséquilibre se produit.
1. Si la différence de hauteur est égale à 2 (déséquilibre du côté gauche) :
-
Condition : hauteur(noeud_gauche) - hauteur(noeud_droit) = 2 -
Cela signifie que le sous-arbre gauche est trop profond par rapport au sous-arbre droit. Il faut appliquer une rotation pour rééquilibrer l'arbre selon la condition suivante :
-
Si le sous-arbre gauche du nœud gauche est plus profond que le sous-arbre droit du nœud gauche, cela implique un déséquilibre gauche-gauche. On effectue une rotation droite pour rééquilibrer l'arbre.
-
Sinon, si le sous-arbre droit du nœud gauche est plus profond que le sous-arbre gauche du nœud gauche, cela implique un déséquilibre gauche-droit. On commence par une rotation gauche sur le nœud gauche, puis on effectue une rotation droite sur le nœud actuel.
-
2. Si la différence de hauteur est égale à -2 (déséquilibre du côté droit) :
-
Condition : hauteur(noeud_droit) - hauteur(noeud_gauche) = 2 -
Cela signifie que le sous-arbre droit est trop profond par rapport au sous-arbre gauche. Il faut également effectuer des rotations pour rééquilibrer l'arbre selon la condition suivante :
-
Si le sous-arbre droit du nœud droit est plus profond que le sous-arbre gauche du nœud droit, cela implique un déséquilibre droit-droit. On effectue une rotation gauche pour rééquilibrer l'arbre.
-
Sinon, si le sous-arbre gauche du nœud droit est plus profond que le sous-arbre droit du nœud droit, cela implique un déséquilibre droit-gauche. On commence par une rotation droite sur le nœud droit, puis on effectue une rotation gauche sur le nœud actuel.
-
Question 4 - Dans la classe ABR, écrire la méthode équilibrage qui implémente l'algorithme présenté ci-dessous. La méthode retourne l'ABR après équilibrage.
def equilibrage(self) -> ABR:
pass
Question 5 - Écrire la méthode insertion_avec_equilibrage. Cette méthode effectue la même chose que la méthode insertion en ajoutant l'étape d'équilibrage après chaque insertion.
def insertion_avec_equilibrage(self, valeur):
pass
Question 6 - Essayer vos méthodes grâce au code ci-dessous.
avl = ABR(8)
avl = avl.insertion_avec_equilibrage(11)
avl = avl.insertion_avec_equilibrage(12)
avl = avl.insertion_avec_equilibrage(15)
avl = avl.insertion_avec_equilibrage(21)
avl = avl.insertion_avec_equilibrage(17)
avl = avl.insertion_avec_equilibrage(22)
avl.affiche()
print('HAUTEUR : ', avl.hauteur())
abr = ABR(8)
abr.insertion_liste([11,12,15,21,17,22])
print('HAUTEUR : ', abr.hauteur())
Si tout fonctionne correctement, un ABR utilisant la méthode d'insertion avec équilibrage (comme dans les arbres AVL) devrait avoir une hauteur inférieure à celle d'un arbre binaire de recherche où les valeurs ont été ajoutées sans équilibrage.