¶ Exercice 1 - Des personnages
Dans cet exercice, on s'intéresse aux personnages d'un jeu. On y retrouve deux types personnages :
- Les fantassins, indiqués par le terme « Fantassin » dans le jeu d'apprentissage.
- Les chevaliers, indiqués par le terme « Chevalier » dans le jeu d'apprentissage.
Chaque personnage possède deux caractéristiques :
- Un niveau force, symbolisé par un nombre entier entre 0 et 20.
- Un niveau de courage, symbolisé par un nombre entier entre 0 et 20.
On met à disposition le jeu d'apprentissage suivant composé de 33 personnages dont on connait leur type et leurs caractéristiques.
L'objectif est de déterminer le type d'un nouveau personnage dont on fournit les caractéristiques de force et de courage.
¶ Introduction
Dans cet exercice, un personnage est représenté par un dictionnaire. Chaque clé correspond à l'une de ses caractéristiques.
Question 1 - Écrire la fonction importer_donnees. Cette fonction prend en paramètre un nom de fichier csv. Elle renvoie une liste de personnages représentés sous la forme d'un dictionnaires. On y retrouver leur nom, leur force, leur courage et leur type.
Pour vous aider, vous pouvez :
- Utiliser le module python
csvet la classeDictReader. - Il faudra utiliser la fonction
openpour ouvrir le fichiercsv. - Le fichier
personnages.csvutilise l'encodeutf-8-sig
def importer_donnees(nom_fichier:str) -> list :
return
Question 2 - Écrire la fonction est_present. Cette fonction prend en paramètre une liste de personnages sous la forme d'une liste de dictionnaires et le nom d'un personnage. Elle retourne True si le personnage est présent dans la liste, False sinon.
def est_present(personnages:list, nom:str) -> bool:
return
Question 3 - Essayer la fonction avec le personnage « Karl » qui est présent dans la liste.
¶ Représentation graphique du jeu d'apprentissage
Il est possible de représenter graphiquement la problématique de cet exercice. Pour cela, nous allons placer chaque personnage sur un repère orthonormé à l'aide du module matplotlib.
Le code ci-dessous montre l'utilisation du module matplotlib pour générer un exemple de graphique.
import matplotlib.pyplot as plt
# Données du type 1
liste_x_1=[1,3,8,13]
liste_y_1=[28,27.2,37.6,40.7]
# Données du type 2
liste_x_2=[2,3,10,15]
liste_y_2=[30,26,39,35.5]
plt.xlabel('Caractéristique 1')
plt.ylabel('Caractéristique 2')
plt.title('Représentation des deux types')
plt.axis('equal') # Pour avoir un repère orthonormé
plt.grid()
plt.scatter(liste_x_1,liste_y_1, label='type 1')
plt.scatter(liste_x_2,liste_y_2, label='type 2')
plt.legend()
plt.show()
Question 3 - Essayer le programme précédant.
En exécutant ce programme, on obtient le schéma suivant :
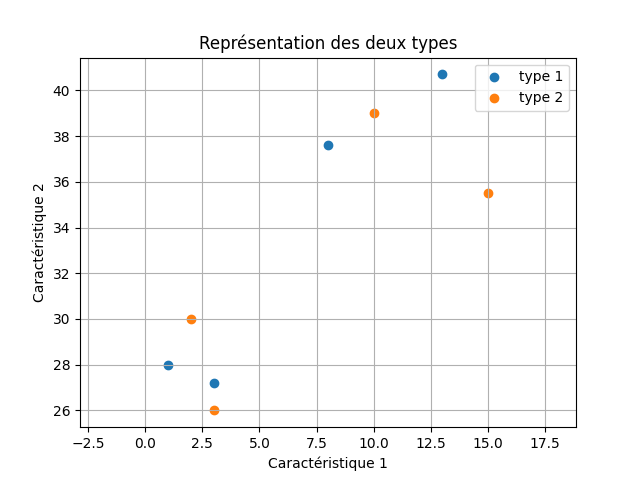
Sur le graphique, chaque entité est placée à l'aide de ses caractéristiques :
- Le caractéristique 1 est sur l'axe des abscisses.
- Le caractéristique 2 est sur l'axe des ordonnées.
Le placement des points sur le graphique se fait à l'aide de la fonction plt.scatter qui prend en paramètre deux listes : les positions en abscisses et les positions en ordonnées.
Question 4 - Écrire une fonction position_abscisse. Cette fonction prend en paramètre une liste de personnages sous la forme d'une liste de dictionnaires et un type de personnage. Elle renvoie la liste des positions en abscisse de chaque personnage correspondant au type passé en paramètre.
- Ici, ce sera le nombre correspondant à la force du personnage.
- Il faudra convertir ce nombre en
int.
def position_abscisse(personnages:list, type:str) -> list:
return
Question 5 - Écrire une fonction position_ordonnee. Cette fonction prend en paramètre une liste de personnages sous la forme d'une liste de dictionnaires et un type de personnage. Elle renvoie la liste des positions en ordonnée de chaque personnage correspondant au type passé en paramètre.
- Ici, ce sera le nombre correspondant au courage du personnage.
- Il faudra convertir ce nombre en
int.
def position_ordonnee(personnages:list, type:str) -> list:
return
Question 6 - Écrire une fonction dessin. Cette fonction prend en paramètre une liste de personnages sous la forme d'une liste de dictionnaires. Elle génère un graphique où chaque personnage du jeu d'apprentissage est représenté par un point.
def dessin(personnges:list) -> None :
pass
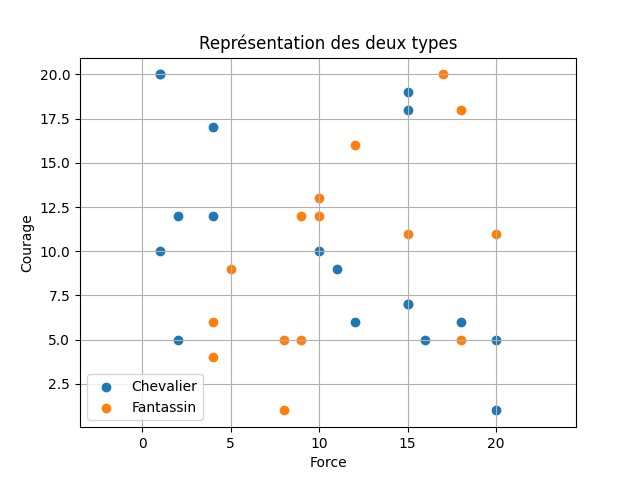
Vous devez obtenir ce schéma suivant :
¶ Algorithme des k plus proches voisins
Attaquons maintenant l'écrire de l'algorithme. On considère un nouveau personnage dont les caractéristiques sont les suivantes :
- Nom : « Lokki »
- Force : 12
- Courage : 13
Sur notre schéma, le nouveau personnage apparait selon un point vert.
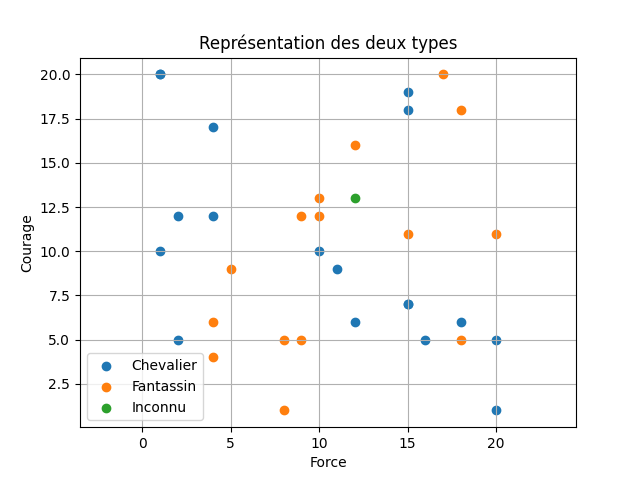
La première étape consiste à calculer la distance entre ce nouveau point et tous les autres points du schéma.
Question 7 - Écrire une fonction distance_euclidienne_2D. Cette fonction prend en paramètre deux points représentés sous la forme d'un tuple. Elle renvoie le résultat du calcul de la distance euclidienne.
def distance_euclidienne_2D(point1:tuple, point2:tuple) -> float:
return
À l'aide la fonction distance, du jeu d'apprentissage et des caractéristiques de la nouvelle valeur, vous êtes capable d'écrire l'algorithme des k plus proches voisins.
Question 8 - Écrire la fonction knn (pour k-nearest neighbors). Cette fonction prend en paramètre une liste de personnages sous la forme d'une liste de dictionnaires, une nouvelle valeur sous la forme d'un tuple et un nombre de voisins.
Elle renvoie la liste des k plus proches voisins.
def knn(personnages:list, n:tuple, k:int) -> list:
return;
Question 9 - Écrire la fonction classification. Elle prend en paramètre une liste de voisins. Elle renvoie la classe majoritaire parmi les voisins.
def classification(liste_voisins:list) -> str:
return
Question 10 - Essayer votre fonction avec des valeurs pour k différentes.
- Pour k=3, la classe choisie est « Fantassin ».
- Pour k=9, la classe choisie est « Fantassin ».
- Pour k=15, la classe choisie est « Chevalier ».
¶ Exercice 2 - Le Choixpeau
À l’entrée à l’école de Poudlard, le Choixpeau magique répartit les élèves dans les différentes maisons (Gryffondor, Serpentard, Serdaigle et Poufsouffle) en fonction de leur courage, leur loyauté, leur sagesse et leur malice.
Le Choixpeau magique dispose d’un fichier csv dans lequel sont répertoriées les données d’un échantillon d’élèves.
Question 1 - Écrire une fonction importer_donnees. Elle prend en paramètre le nom du fichier csv. Elle renvoie une liste de dictionnaire représentant les élèves présents dans le fichier csv avec toutes les caractéristiques.
def importer_donnees(nom_fichier:str) -> list :
return
On souhaite analyser le contenu du fichier csv.
Question 2 - Écrire une fonction frequence_maisons. Cette fonction prend en paramètre une liste d'élèves sous la forme d'une liste de dictionnaires. Elle renvoie le dictionnaire des fréquences des maisons.
def frequence_maisons(liste:list) -> dict:
return
Vous devez obtenir :
{'Serpentar': 12, 'Gryffondor': 17, 'Serdaigle': 11, 'Poufsouffle': 10}.
Question 3 - Écrire une fonction maison_majoritaire. Cette fonction prend en paramètre une table d'élèves. Elle renvoie le nom de la maison la plus représentée.
def maison_majoritaire(liste:list) ->str:
return
On s'intéresse maintenant à l'algorithme des k plus proches voisins. On souhaite déterminer la maison des 4 élèves suivants :
| Nom | Courage | Loyauté | Sagesse | Malice |
|---|---|---|---|---|
| Hermione | 8 | 6 | 6 | 6 |
| Drago | 6 | 6 | 5 | 8 |
| Cho | 7 | 6 | 9 | 6 |
| Cédric | 7 | 10 | 5 | 6 |
Question 4 - Écrire une fonction distance_manhattan. Cette fonction prend en paramètre deux élèves représentés sous la forme d'un dictionnaire. Elle renvoie le résultat du calcul de la distance de Manhattan entre ces deux élèves.
def distance_manhattan(d1:dict, d2:dict) -> float:
return
Question 5 - Vérifier que la distance de Manhattan entre Hermione et Adrian est égale à 8.
Question 6 - Écrire la fonction knn (pour k-nearest neighbors). Cette fonction prend en paramètre une liste d'élèves sous la forme d'une liste de dictionnaires, un nouvel élève sous la forme d'un dictionnaire et un nombre de voisins.
Elle renvoie la liste des k plus proches voisins.
def knn(eleve:list, n:tuple, k:int) -> list:
return;
Question 7 - Écrire la fonction classification. Elle prend en paramètre une liste de voisins. Elle renvoie la classe majoritaire parmi les voisins.
def classification(liste_voisins:list) -> str:
return
La maison attribuée pour « Hermione » est « Gryffondor ».
Question 8 - Exécuter la fonction pour les 3 autres élèves dont il faut trouver la maison.
¶ Exercice 3 - Pokémon
Vous avez à disposition un fichier csv dans lequel on retrouve environ 400 Pokémon répartis selon 18 types.
On souhaite trouver le type d'un nouveau Pokémon selon ses caractéristiques suivantes :
- Point de vie : 108
- Attaque : 112
- Défense : 118
- Vitesse : 47
Question 1 - À l'aide des exercices précédents, déterminer le type de ce nouveau Pokémon en utilisant l'algorithme des k plus proches voisins.
- Vous ferez les tests avec la distance euclidienne et la distance de Manhattan.
- Vous utilisez plusieurs valeurs pour k afin d'observer les changements de classification.
¶ Exercice 4 - Rugby
Nous allons voir comment l'algorithme des k plus proches voisins peut nous aider à prévoir quel poste pourrait être proposé à un nouveau joueur de rugby, uniquement d'après sa masse et sa taille.
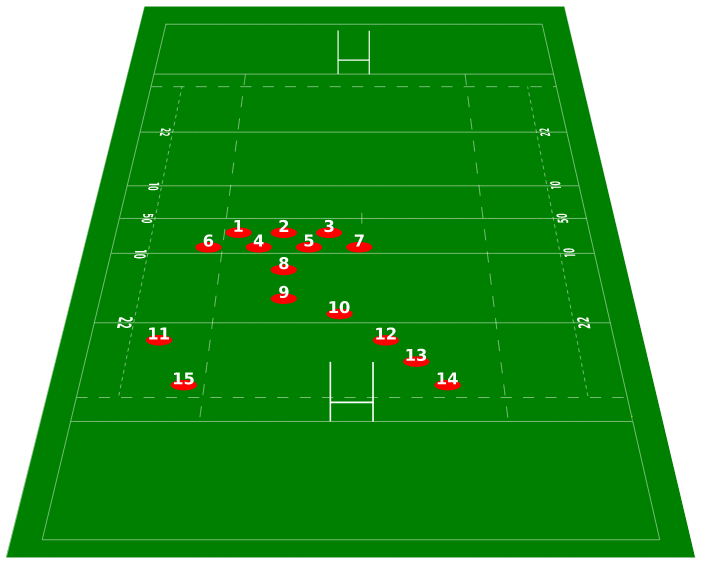
Avant toute chose, il peut être important d'énumérer les différents postes existants au rugby. Cette illustration peut vous aider :
Cet algorithme nécessite un jeu de données, le plus large possible. Nous utiliserons les données mises à disposition par l'organisation « Six Nations Rugby Limited ». Ces données concernent les équipes des hommes sur la saison 2020-2021, et sont compilées dans le fichier ci-dessous.
Question 1 - Écrire une fonction importer_donnees. Elle prend en paramètre le nom du fichier csv. Elle renvoie une liste de dictionnaire représentant les joueurs présents dans le fichier csv avec toutes leurs caractéristiques.
def importer_donnees(nom_fichier:str) -> list :
return
Question 2 - En s'inspirant de l'exercice 1 et en utilisant le module matplotlib, générer le schéma suivant montrant la répartition des postes en fonction de la taille et de la masse des joueurs.
Vous devez obtenir le résultat suivant :
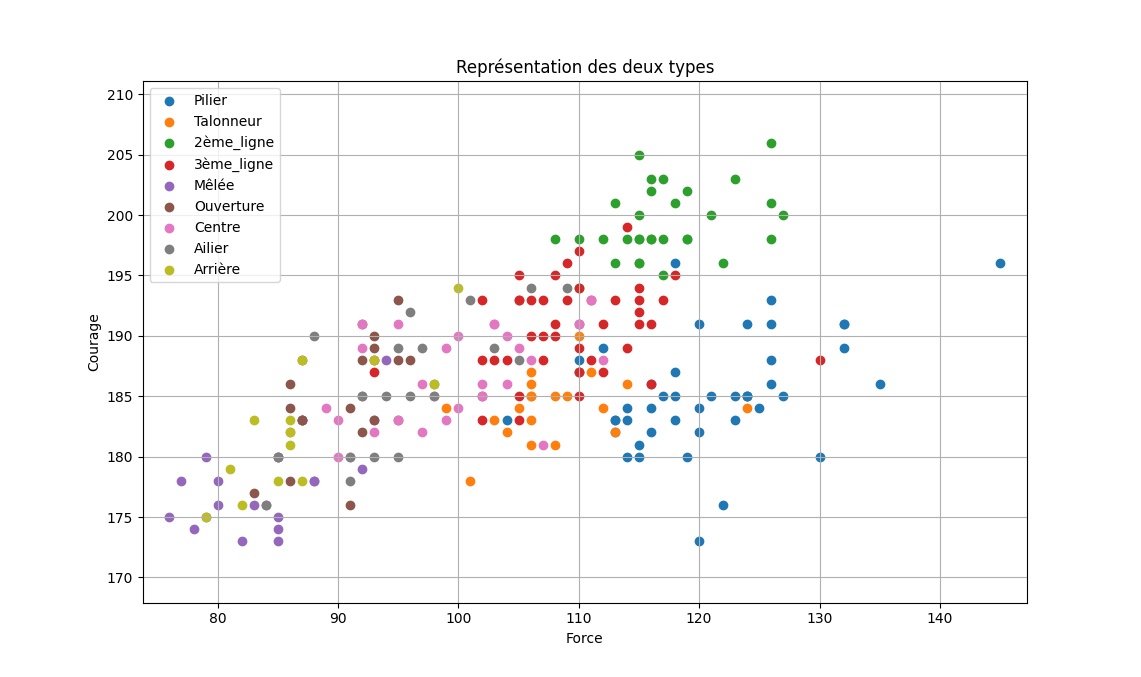
Un nouveau joueur, John, vient intégrer l'équipe. Il faut lui trouver un poste. Voici ces caractéristiques :
- Taille : 1m89
- Masse : 102 kg.
Question 3 - À l'aide des exercices précédents, déterminer le poste de ce nouveau joueur en utilisant l'algorithme des k plus proches voisins.
- Vous ferez les tests avec la distance euclidienne.
Question 4 - Effectuer les tests suivants avec des valeurs de k différentes :
k=1: John est un aillier.k=3: John est un 3ème ligne.k=9: John est un centre.k= tous ses voisins: John est un pillier.
Dans le dernier exemple, il est inutile de consulter le graphique. Il suffit de trouver quel poste est le plus présent dans la base de donnée et on pourrait alors en déduire le poste de John.
On a vu que la détermination d'une catégorie à l'aide de l'algorithme des k plus proches voisins dépend énormément du choix de k, le nombre de voisins.
Pour limiter les cas d'égalité, on rappelle qu'il est intéressant de choisir une valeur de k impaire, surtout dans les situations où l'on a que deux catégories à différencier.