¶ Vidéo passionnante pour découvrir
- Le jeu de la vie (ORIGINALE)Vidéo Youtube de EGO
- Le jeu de la vie (REACT Domingo) Même vidéo, mais commentée par le streamer Domingo
- Rendu du travail
¶ Introduction
L'objectif de ce projet de réaliser un programme permettant de simuler le jeu de la vie. Ce jeu a été inventé par le mathématicien britannique John H. Conway (1937-2020). Il représente est une simulation de l'évolution d'une population de cellules modélisées par un programme informatique.

¶ Règles du jeu
Le Jeu de la vie est un « jeu à zéro joueur » en mode tour à tour. Il est défini comme jeu à zéro joueur, car il ne nécessite aucune intervention lors de son déroulement.
Il s’agit d’un automate cellulaire, un modèle où chaque état conduit mécaniquement à l’état suivant à partir de règles préétablies.
-
Le jeu se déroule sur une grille à deux dimensions, théoriquement infinie, dont les cases, que l'on appelle « cellules » peuvent prendre deux états distincts : « vivante » ou « morte ».
-
Chaque cellule possède 8 voisines, qui sont les cellules adjacentes horizontalement, verticalement et diagonalement.
-
À chaque tour de jeu, l'état d’une cellule est complétement déterminée par l’état de ses huit cellules voisines, selon les règles suivantes bien définie, que l'on appelle « règles d'évolution ».
¶ Règles d'évolution
Ce jeu repose sur deux règles relativement simples :
- Une cellule morte possédant exactement trois cellules voisines vivantes devient vivante au tour suivant.
- Une cellule vivante possédant deux ou trois cellules voisines vivantes reste vivante, sinon elle meurt au tour suivant.
¶ Représentation des cellules
La grille d'une génération est un tableau à deux dimensions, que l'on représentera par une liste de listes en Python. Chaque élément de cette liste représente une cellule qui peut prendre deux états :
- L'état
False, qui indique que la cellule est morte. - L'état
True, qui indique que la cellule est vivante.
Ainsi, on obtient la représentation suivante pour une grille de 4x3.
False True False False
False False False False
False False False True
¶ Cases voisines
De plus, chaque case de la grille possède un nombre de cases voisines compris entre 3 (si c'est un coin) et 8 (si elle n'est pas sur le bord de la grille). Chaque case voisine peut être vivante ou morte.
Voici un exemple d'évolution passant d'une génération à .

Pour avoir plus d'informations sur le fonctionnement du jeu de la vie, vous pouvez regarder les ressources suivantes :
¶ Étapes de construction
L'objectif de ce projet de réaliser un programme permettant de simuler le jeu de la vie. Pour y arriver, voici un ensemble de fonctions à écrire.
¶ Partie 1 - Gestion de la grille
Dans cette première partie, on s'intéresse à la représentation de la grille dans laquelle évoluera le jeu. Pour rappel, la grille est représentée par une liste à deux dimensions contenant des booléens.
Question 1 - Écrire une fonction generer_grille. Cette fonction prend en paramètre deux entiers positifs correspondant au nombre de lignes et au nombre de colonnes d'une grille du jeu de la vie. Cette fonction retourne une liste de listes représentant une grille.
def generer_grille(hauteur:int, largeur:int) -> list:
return
Question 2 - Écrire une fonction largeur. Cette fonction prend en paramètre une liste représentant la grille de jeu. Elle retourne la largeur de cette grille.
def largeur(grille:list) -> int:
return
Question 3 - Écrire une fonction hauteur. Cette fonction prend en paramètre une liste représentant la grille de jeu. Elle retourne la hauteur de cette grille.
def hauteur(grille:list) -> int:
return
Question 4 - Écrire une fonction afficher. Cette fonction qui prend en paramètre une liste représentant la grille de jeu. Elle affiche cette grille selon le format suivant :
- Le symbole
Xindique que la cellule est vivante - Le symbole
espaceindique que la cellule est morte
def afficher(grille:list) -> None:
Voici un aperçu du résultat attendu par la fonction.
| | |X|X|X|
|X|X|X|X|X|
|X|X| |X|X|
| |X| |X|X|
|X|X| | |X|
|X|X| | |X|
| |X|X| | |
|X|X|X| |X|
|X|X|X|X|X|
| | |X|X| |
Question 5 - Écrire une fonction remplir. Cette fonction prend en paramètre une liste représentant la grille de jeu et une probabilité sous la forme d'un float (entre 0 et 1). Elle parcourt la grille et la modifie en plaçant des cellules vivantes selon la probabilité passée en paramètre.
- Vous devez utiliser le module
randomafin de générer un nombre aléatoire. - Si le nombre choisi aléatoirement est inférieur à la probabilité, il faut placer une cellule vivante.
- Sinon, il faut placer une cellule morte.
def remplir(grille:list, proba:float) -> None:
return
Cette fonction ne renvoie rien, mais modifie directement le paramètre
grille. On dit que cette fonction produit un « effet de bord » sur le paramètregrille.
À la fin de cette question, vous êtes capable de créer et d'afficher une grille du jeu de la vie.
¶ Partie 2 - Gestion des cellules
Dans cette seconde partie, on s'intéresse à la gestion des cellules présente sur la grille du jeu de la vie.
Question 6 - Écrire une fonction est_valide. Cette fonction prend en paramètre une liste à deux dimensions représentant la grille de jeu et deux nombres entiers x et y représentant la position d'une cellule selon ses coordonnées et . Elle retourne True si les indices de la cellule sont bien compris dans la grille, False sinon.
def est_valide(grille:list, x:int, y:int) -> bool:
return
Question 7 - Écrire une fonction est_vivante. Cette fonction prend en paramètre une liste à deux dimensions représentant la grille de jeu et deux nombres entiers x et y représentant la position d'une cellule selon ses coordonnées et . Elle retourne True si la cellule est vivante, False si la cellule est morte.
def est_vivante(grille:list, x:int, y:int) -> bool:
return
Question 8 - Écrire une fonction cases_voisines. Cette fonction prend en paramètre une liste à deux dimensions représentant la grille de jeu et deux nombres entiers x et y la position d'une cellule selon ses coordonnées et . Cette fonction retourne la liste des cellules voisines/ Les cellules seront identifiées sous la forme d'un tuple (x, y).
- On ajoutera dans la liste uniquement les cellules valides.
def cases_voisines(grille:list, x:int, y:int) -> list:
return
Question 9 - Écrire une fonction cases_voisines_vivantes. Cette fonction prend en paramètre une liste à deux dimensions représentant la grille de jeu et deux nombres entiers x et y la position d'une cellule selon ses coordonnées et .
Cette fonction retourne la liste des cellules voisines vivantes, parmi les toutes les cellules voisins. Les cellules seront identifiées sous la forme d'un tuple (x, y).
def cases_voisines_vivantes(grille:list, x:int, y:int) -> list:
return
À la fin de cette question, il est possible, pour chaque cellule, de récupérer les listes des voisines vivantes.
¶ Étape 3 - Gestion des générations
Dans cette troisième partie, on s'intéresse à création des générations suivantes (passer du tour au tour ).
Question 10 - Écrire une fonction generation_suivante. Cette fonction prend en paramètre une liste à deux dimensions représentant la grille de jeu. Elle retourne une nouvelle liste à deux dimensions représentant la grille de jeu de la génération suivante, en suivant les règles d'évolutions :
- Une cellule vivante reste en vie si elle a 2 ou 3 voisines vivantes.
- Une cellule morte nait si elle a exactement 3 voisines vivantes.
def generation_suivante(grille:list) -> list:
return
Cette fonction ne modifie pas la grille courante, mais crée une nouvelle grille. Il faut donc créer une nouvelle grille vide aux mêmes dimensions que la grille de départ dans laquelle on placera les cellules mortes ou vivantes selon les règles ci-dessus.
¶ Étape 4 - Animation Version 1
Sur cette dernière étape, on s'intéresse au lancement du jeu, afin de voir l'évolution de la grille tour par tour.
Question 11 - Écrire une fonction animation. Cette fonction prend en paramètre une liste représentant une grille et un nombre entier représentant le nombre de générations à afficher. Cette fonction affiche les générations successives issues de la grille de départ.
def animation(grille:list, nb_gen:int) -> None:
return
¶ Étape 5 - Animation V2 avec Tkinter
Pour cette dernière étape, vous utiliserez un fichier Python qui permet d'animer la grille de jeu dans une fenêtre graphique. Ce fichier utilise le module Tkinter.
Question 12 - Renommer votre fichier avec toutes les fonctions précédentes en jeudelavie.py.
Question 13 - Créer un nouveau fichier nommé graphique.py et y ajouter le code suivant :
from tkinter import *
from jeudelavie import *
fenetre = Tk()
WIDTH = 800
HEIGHT = 800
fenetre.title("Ma fenêtre")
canva = Canvas(fenetre, width=WIDTH, height=HEIGHT, bg="black")
canva.pack(padx=0, pady=0)
grille = generer_grille(50,50)
remplir(grille, 0.5)
def afficher():
global grille
grille = generation_suivante(grille)
canva.delete("all")
size = WIDTH // len(grille)
for y in range(len(grille[0])):
for x in range(len(grille)):
x1, y1,= x*size, y*size
x2, y2 = x1 + size, y1 + size
if grille[x][y]:
canva.create_rectangle(x1, y1, x2, y2 , fill='white', width=0)
else:
canva.create_rectangle( x1, y1, x2, y2 , fill='black',width=0)
canva.after(50, afficher)
afficher()
fenetre.mainloop()
Question 14 - Exécuter ce programme et observer l'évolution des générations.

¶ Étape 6 - Essayer quelques schémas
Dans la vidéo d'EGO, on parle de nombreuses structures que l'on peut retrouver au sein de la grille de jeu.
- Les structures stables : Ce sont des ensembles de cellules ayant stoppé toute évolution : elles sont dans un état stationnaire et n’évoluent plus tant qu’aucun élément perturbateur n’apparaît dans leur voisinage. Un bloc de quatre cellules est la plus petite structure stable possible.

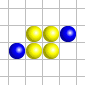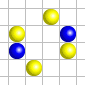
- Les oscillateurs : Ce sont des structures qui se transforment de manière cyclique, en revêtant plusieurs formes différentes avant de retrouver leur état initial. Des figures de ce type sont très nombreuses : on en connaît actuellement des centaines. La « grenouille » est une structure qui se répète toutes les deux générations.
- Les vaisseaux : Ce sont des structures capables, après un certain nombre de générations, de produire une copie d’elles-mêmes, mais décalées dans l’univers du jeu.

- Les canons : Les canons sont des configurations qui émettent un autre motif, tel qu'un vaisseau, à intervalles réguliers. Ces vaisseaux sont des motifs qui continuent de se déplacer sur la grille de jeu. La périodicité des canons, soit l'intervalle de temps après lequel ils répètent leur comportement, peut varier.
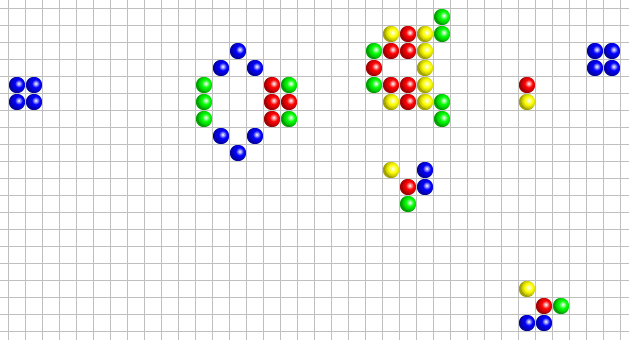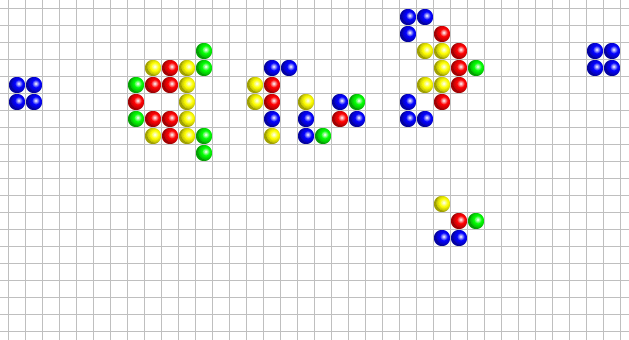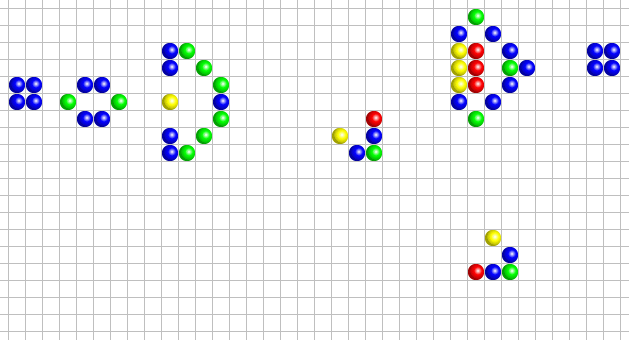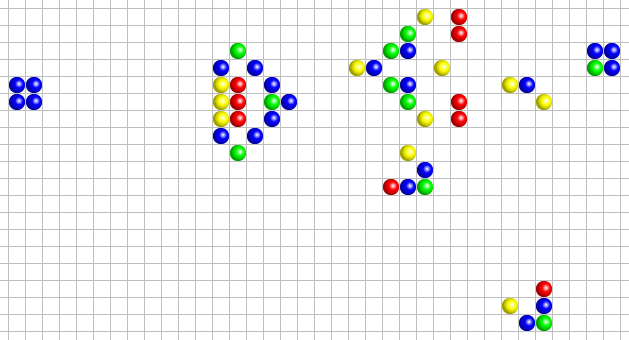
Question 15 - À l'aide de la vidéo et des exemples présentés ci-dessus, essayer d'implémenter ces différentes structures. Vous pouvez, pour chaque exemple, créer une nouvelle fonction qui permettra de générer la grille de départ, avec au sein de cette grille, la structure choisie.