¶ Simulation avec le logiciel Logisim
L'objectif de cette activité de construire des circuits logiques à l'aide des différents fonctions booléennes découvertes en cours.
Les questions identifiées par le symbole
demande une réponse à écrire sur votre feuille.
Document réponse
¶ Prise en main du logiciel Logisim
¶ Installation
Le logiciel Logisim est un logiciel de simulation de circuits logiques. C’est un logiciel libre et gratuit. Si le logiciel n’est pas installé sur votre ordinateur, vous pouvez l’installer selon les indications suivantes (sur Windows) :
- Téléchager l'application grâce au lien suivant : https://freefr.dl.sourceforge.net/project/circuit/2.7.x/2.7.1/logisim-win-2.7.1.exe?viasf=1
- Suivre les étapes d'installation.
¶ Interface du logiciel
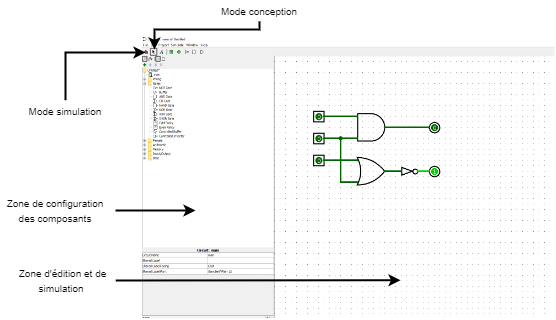
¶ Mode édition
Pour utiliser le mode édition, il faut sélectionner la flèche en haut dans la barre d’outils.
- Pour ajouter un composant, il suffit de le rechercher dans la liste de gauche et de le déposer dans la zone du schéma.
- Les portes logiques sont présentes dans les répertoires
Gates. - Vous pouvez modifier la configuration des composants grâce à la zone en bas à gauche. (modifier le nombre d’entrées, son nom, son orientation…)
- Il est possible d’effectuer des copier/coller des composantes afin de garder la même configuration.
¶ Mode simulation
Pour utiliser le mode simulation, il faut sélectionner la main en haut dans la barre d’outils.
- Il est possible de changer l’état des entrées en cliquant dessus.
- La couleur vert clair des fils indique la valeur 1 et la couleur vert foncé indique la valeur 0.
¶ Exercice 1 - Les portes logiques de base
Question 1 - Construire un circuit qui simule le fonctionnement des portes logiques suivantes :
NOTORANDXOR
Question 2 - Compléter les tables de vérité de chaque fonction.
Question 3 - Donner deux expressions booléennes qui correspondent à la fonction
XOR.
Question 4 - Construire un circuit qui simule le fonctionnement de la porte XOR avec uniquement les portes logiques NOT, OR et AND.
¶ Exercice 2 - Lois de De Morgan
Question 1 - Compléter la table de vérité des fonctions
NOR et NAND.
Question 2 - Construire deux circuits différents qui simulent le fonctionnement de la porte NOR.
Question 3 - Construire deux circuits différents qui simulent le fonctionnement de la porte NAND.
¶ Exercice 3 - Table de vérité
Dans cet exercice, on considère la table de vérité suivante :
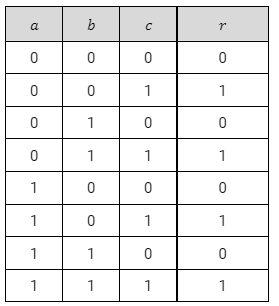
Question 1 - Écrire l'expression booléenne issue de la table de vérité ci-dessus.
Question 2 - Construire un circuit représentant l'expression de la table de vérité ci-dessus.
Question 3 - Simplifier l'expression obtenue à la question 1.
¶ Exercice 4 - Expression booléenne
Dans cet exercice, on considère l'expression booléenne suivante :
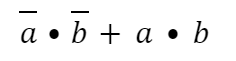
Question 1 - Écrire la table de vérité de cette expression.
Question 2 - Construire un circuit représentant l'expression ci-dessus uniquement avec les portes NOT, AND et OR.
¶ Exercice 5 - NOR et NAND
¶ Partie 1 - NOR
Question 1 - Construire un circuit représentant une porte NOT uniquement avec des portes NOR.
Question 2 - Construire un circuit représentant une porte OR uniquement avec des portes NOR.
Question 3 - Construire un circuit représentant une porte AND uniquement avec des portes NOR.
¶ Partie 2 - NAND
Question 4 - Construire un circuit représentant une porte NOT uniquement avec des portes NAND.
Question 5 - Construire un circuit représentant une porte OR uniquement avec des portes NAND.
Question 6 - Construire un circuit représentant une porte AND uniquement avec des portes NAND.
Les portes
NANDetNORsont dites universelles.
¶ Exercice 6 - Comparateur 2 bits
On considère un circuit combinatoire qui possède 2 entrées et et 3 sorties , et . Ce circuit permet de comparer 2 bits :
- Si le bit est plus grand que le bit , alors
- Si le bit est plus petit que le bit , alors
- Si les deux bits et ont la même valeur, alors
Question 1 - Écrire la table de vérité du comparateur 2 bits.
Question 2 - En déduire les expressions booléennes associées à la table de vérité.
Question 3 - Construire un circuit représentant les expressions ci-dessus. (3 entrées, 2 sorties).
¶ Exercice 7 - Additionneur binaire
¶ Partie 1 : Le demi-additionneur
Dans cet exercice, on souhaite créer un circuit pour calculer le résultat de l'addition entre deux nombres d'un seul bit.
Le circuit prendra 2 entrées représentant les deux nombres et 2 sorties représentant la somme des bits et la retenue.

Question 1 - Écrire la table de vérité correspondant à l'addition de 2 bits.
Question 2 - Écrire une expression booléenne simplifiée de la table de vérité.
Question 3 - Construire un circuit représentant l'addition de 2 bits.
Ce circuit est appelé un demi-additionneur : Il permet uniquement d'addition de deux nombres d'un seul bit. Pour les nombres plus grands, c'est impossible car il ne prend pas en compte les retenues entrantes, d'où son nom demi-additionneur.
¶ Partie 2 : L'additionneur complet
L'additionneur complet doit donc comporter une entrée supplémentaire qui indique la présence d'une éventuelle retenue.
Question 4 - Écrire la nouvelle table de vérité avec :
- 3 entrées : , et indiquant la retenue.
- 2 sorties : pour la somme et pour la retenue suivante.
Pour construire un additionneur complet, il suffit de relier en cascade plusieurs demi-additionneur. Pour simplifier le schéma général dans Logisim, il est possible de créer des sous-circuit comme le montre l'image suivante.
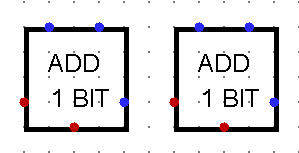
Ces deux circuits sont des demi-additionneurs prenant en compte l'entrée d'une retenue (point bleu sur le côté des schémas).
Question 5 - Créer un nouveau sous-circuit en cliquant sur le bouton vert en haut à gauche et donner un nom à votre circuit.
Question 6 - Construire le circuit du demi-additionneur correspondant à la table de vérité de la question 4 (3 entrées et 2 sorties).
Question 7 - Dans le circuit principal, construire le nouveau circuit correspondant à l'additionneur complet. Vous devrez importer plusieurs fois un demi-additionneur.
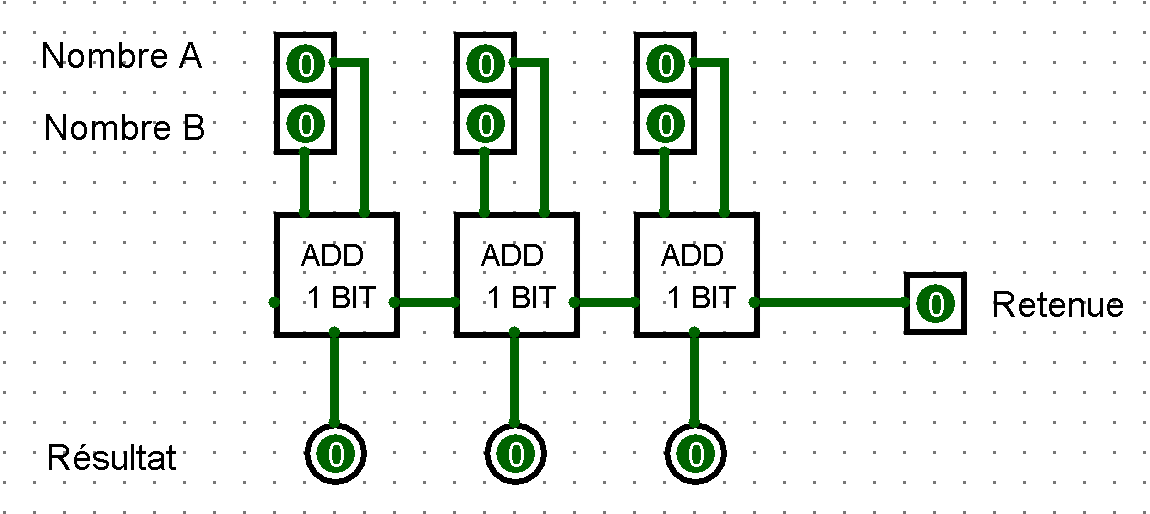
¶ Exercice 8 - L'afficheur 7 segments (pour aller plus loin)
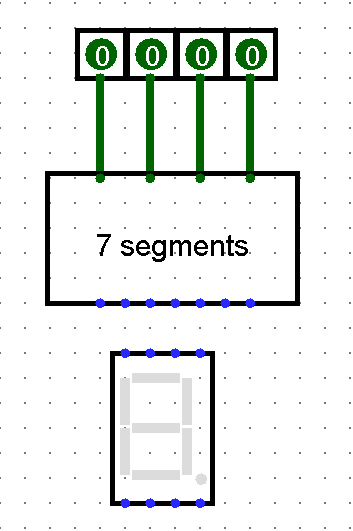
Un afficheur 7 segments est un type d'afficheur qui utilise 7 segments de lumière pour dessiner des chiffres.

Le but de cet exercice est de construire un circuit composé de 4 bits en entrée et 7 sorties.
- Les 4 bits en entrée représentent un nombre décimal écrit en base 2.
- Les 7 sorties sont chacune associées à un segment de l'afficheur.
Exemple :
- Le nombre binaire doit permettre afficher le nombre 0 sur l'afficheur. Ainsi, pour afficher le nombre 0, il faut allumer les segments A, B, C, D, E et F.
Question 1 - Écrire la table de vérité du fonctionnement d'un afficheur 7 segments. Elle sera composée de :
- 4 entrées , , et
- 7 sorties , , , , , et qui correspondent aux différents segments de l'afficheur.
Question 2 - Trouver les expresions simplifiées pour chacune des sorties.
Question 3 - Construire le circuit de l'afficheur 7 segments.
¶ Exercice 8 - Système de vote (pour aller plus loin)
Le comité directeur d’une entreprise est constitué de quatre membres :
- le directeur
- ses trois adjoints A, B, C.
Lors des réunions, les décisions sont prises à la majorité. Chaque personne dispose d’un interrupteur pour voter sur lequel elle appuie en cas d’accord avec le projet soumis au vote. En cas d égalité du nombre de voix, celle du directeur compte double.
On vous demande de réaliser un dispositif logique permettant l’affichage du résultat du vote sur une lampe R.
Question 1 - Dessiner et compléter la table de verité représentant cette situation.
Question 2 - Trouver l’équation logique de R.
Question 3 - Réaliser le schéma logique de la sortie R .