
¶ Partie 1 - Création des fonctions
Dans cette partie, créer un nouveau fichier recherche.py.
¶ Exercice 0 - Une fonction utile
Question 1 - Écrire une fonction generer_liste(n). Cette fonction prend en paramètre un nombre entier n. Elle retourne une liste de n nombres aléatoires choisi entre 0 et 1000. La liste sera triée dans l'ordre croissant.
def generer_liste(n:int) -> list :
¶ Exercice 1 - La recherche naïve
Dans ce premier exercice, on s'intéresse à l'algorithme de recherche naïve.
Question 1 - Écrire une fonction recherche_naive_for qui prend en paramètre une liste et une valeur. Cette fonction retourne l'indice de cette valeur dans le tableau si elle est présente, ou retourne -1 si elle absente.
- Vous devez utiliser une boucle
for
def recherche_naive_for(tab:list, valeur:int) -> int
Question 2 - Écrire une fonction recherche_naive_while qui prend en paramètre une liste et une valeur. Cette fonction retourne l'indice de cette valeur dans le tableau si elle est présente, ou retourne -1 si elle absente.
- Vous devez utiliser une boucle
while
def recherche_naive_while(tab:list, valeur:int) -> int
Question 3 - Modifier vos fonctions afin de retourner le nombre de comparaisons effectuées lors du parcours. La valeur retournée par la fonction sera un tuple (indice, nb_comparaison).
¶ Exercice 2 - La recherche dichotomique
Question 1 - Écrire une fonction recherche_dicho qui prend en paramètre une liste et une valeur. Cette fonction retourne l'indice de cette valeur dans le tableau si elle est présente, ou retourne -1 si elle absente.
- Cette fonction utilise le principe de la dichotomie.
def dichotomie(tab:list, valeur:int) -> int:
On rappelle ci-dessous l'algorithme en pseudo-code de la recherche dichotomique :
valeur ← ……………
t ← [1,3,4,6,7,9,10,13,15,18]
debut <- 0
fin <- longueur(t) - 1
TANT QUE debut <= fin
m = (debut + fin) // 2
SI t[m] == valeur ALORS
RETOURNER Vrai
SINON
SI t[m] < valeur ALORS
debut <- m+1
SINON
fin <- m-1
FIN SI
FIN SI
FIN TANTQUE
RETOURNER Faux
Question 2 - Modifier vos fonctions afin de retourner le nombre de comparaisons effectuées lors du parcours. La valeur retournée par la fonction sera un tuple (indice, nb_comparaison).
¶ Partie 2 - Analyse du nombre de comparaisons
Dans cette partie, on s'intéresse à l'efficacité de notre programme en comptant le nombre de comparaisons de chaque fonction.
L'objectif est de générer une courbe du nombre de comparaisons à effectuer en fonction de la taille du tableau.
Dans un premier temps, créer un fichier analyse_nombre.py dans lequel vous allez importer vos fonctions grâce à la ligne suivante.
from recherche import generer_liste, recherche_naive_for, dichotomie
¶ Exercices
Question 1 - Écrire une fonction essais_recherche_naive(taille_liste_max). Cette fonction permet de générer une liste de valeurs correspondant au nombre de comparaisons à effectuer en fonction de la taille du tableau.
Cette fonction prend en paramètre un nombre entier correspondant à la taille maximale d'un tableau. Cela veut dire qu'on testera la fonction avec un tableau de taille 1, 2, 3... jusqu'à la taille passée en paramètre.
- Le nombre de comparaisons de chaque essai sera ajoutée dans une liste.
- Le nombre à rechercher sera -1 pour simuler le pire des cas
def essais_recherche_naive(taille_liste_max)
'''
>>> essais_recherche_naive(10)
[1, 2, 3, 4, 5, 6, 7, 8, 9]
'''
Question 2 - Écrire une fonction essais_recherche_dicho(taille_liste_max). Cette fonction permet de générer une liste de valeurs correspondant au nombre de comparaisons à effectuer en fonction de la taille du tableau.
Sur le même principe que la question précédente, le nombre passé en paramètre correspond à la taille maximale d'un tableau.
- Le nombre de comparaisons de chaque essai sera ajoutée dans une liste.
- Le nombre à rechercher sera -1 pour simuler le pire des cas
def essais_recherche_dicho(taille_liste_max)
'''
>>> essais_recherche_dicho(10)
[1, 1, 2, 2, 2, 2, 3, 3, 3]
'''
Question 3 - Les deux fonctions précédentes génèrent une liste de nombre de comparaisons effectuées en fonction de la taille d'un tableau. On peut ainsi comparer l'efficacité des deux algorithmes de recherche en dessinant un graphique grâce au module pylab.
Si le module
pylabn'est pas intallé, utilisez la commandepip install matplotlib.
Pour dessiner une courbe, il faut d'abord récupérer une liste ou plusieurs listes de valeurs.
TAILLE_MAX_LISTE = 1000
y1 = essais_recherche_naive(TAILLE_MAX_LISTE)
y2 = essais_recherche_dicho(TAILLE_MAX_LISTE)
On peut ensuite utiliser la fonction plot du module pylab afin de dessiner une courbe.
pylab.plot(y1,color='r', label="naive")
pylab.plot(y2,color='b', label="dicho")
pylab.show()
Normalement, une fenêtre s'ouvre avec les deux courbes.
.png)
¶ Partie 3 - Analyse du temps d'exécution
Dans cette partie, on s'intéresse à l'efficacité de notre programme en mesurant le temps d'exécution de chacun des algorithmes. Pour cela, nous allons utiliser le module timeit.
L'objectif est de générer une courbe qui affiche le temps d'exécution en fonction de la taille du tableau.
Dans un premier temps, créer un nouveau fichier analyse_temps.py avec les différents modules nécessaires.
from timeit import timeit
import pylab
¶ Le module timeit
Le module timeit de Python permet de prendre une mesure du temps d'exécution d'une fonction, en secondes. Ce module fournit une fonction timeit qui accepte en entrée trois paramètres :
-
setuppermet de préciser àtimeitles modules à charger pour permettre l'exécution correcte de la fonction (y compris donc le module qui contient la fonction à mesurer), -
stmt– pour statement, est l'appel de la fonction qui sera mesurée, avec ses paramètres -
numberest le nombre de fois où l'instructionstmtsera exécutée. Le temps mesuré sera le temps cumulé pour toutes ces exécutions.
Remarquez que le code Python des deux paramètres setup et stmt sont donnés sous forme d'une chaîne de caractères. Par exemple, après avoir importé le module timeit :
from timeit import timeit
On peut mesurer le temps d'exécution d'une fonction puissance :
imports = "from .... import ...."
program = "ma_fonction(4, 12)"
temps = timeit(setup=imports, stmt=program, number=100)
Le résultat obtenu représente le temps total mis pour exécuter 100 fois ma_fonction.
¶ Exercices
Question 1 - Écrire une fonction temps_recherche_naive qui prend en paramètre 2 entiers taille_liste et nb_repetitions. Cette fonction utilise la fonction timeit et renvoie le temps en seconde de la recherche naïve avec une liste dont la taille est passée en paramètre.
def temps_recherche_naive(taille_liste, nb_repetitions):
Question 2 - Écrire une fonction temps_recherche_dicho qui prend en paramètre 2 entiers taille_liste et nb_repetitions. Cette fonction utilise la fonction timeit et renvoie le temps en seconde de la recherche dichotomique avec une liste dont la taille est passée en paramètre.
def temps_recherche_dicho(taille_liste, nb_repetitions):
Pour les deux questions suivantes, on souhaite obtenir une liste de valeur correspondant au temps d'exécution en fonction de la taille du tableau.
Question 3 - Écrire une fonction courbe_recherche_naive. Cette fonction retourne une liste des différents temps d'exécution en fonction de la taille du tableau. Elle fait appel à la fonction temps_recherche_naive. On se basera sur 100 répétitions
Elle prend en paramètre un nombre entier correspondant à la taille maximale d'un tableau. Cela veut dire qu'on testera la fonction avec un tableau de taille 1, 2, 3... jusqu'à la taille passée en paramètre.
- Le temps de chaque essai sera ajoutée dans une liste.
- Le nombre à rechercher sera -1 pour simuler le pire des cas
def courbe_recherche_naive(taille_liste):
Question 4 - Écrire une fonction courbe_recherche_dicho. Cette fonction retourne une liste des différents temps d'exécution en fonction de la taille du tableau. Elle fait appel à la fonction temps_recherche_dicho. On se basera sur 100 répétitions
Elle prend en paramètre un nombre entier correspondant à la taille maximale d'un tableau. Cela veut dire qu'on testera la fonction avec un tableau de taille 1, 2, 3... jusqu'à la taille passée en paramètre.
- Le temps de chaque essai sera ajoutée dans une liste.
- Le nombre à rechercher sera -1 pour simuler le pire des cas
def courbe_recherche_dicho(taille_liste):
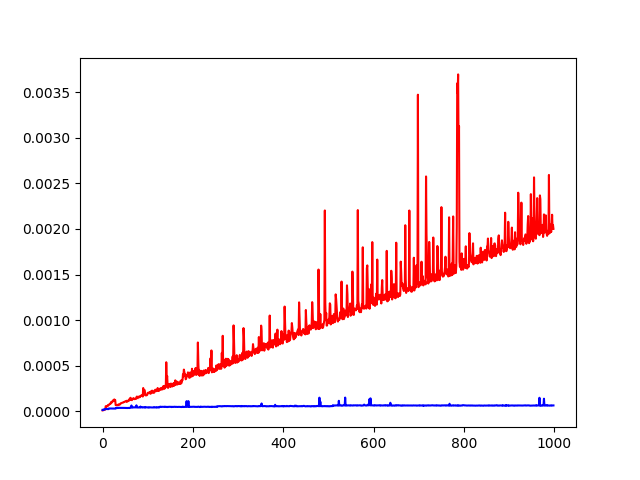
Question 5 - Sur le même principe que la partie 2, dessiner la courbe avec le temps d'exécution des deux algorithmes en fonction de la taille d'un tableau.
¶ Partie 4 - Exercices
¶ Exercice 1 - Plus ou moins
Question 1 - Écrire une fonction deviner_nombrequi prend un nombre entier en paramètre. Cette fonction tire un nombre au hasard entre 0 et puis demande à l'utilisateur de deviner ce nombre.
À chaque essai, le programme répond « Plus petit » ou « Plus grand », ou « Trouvé ». La fonction renvoie le nombre de coups utilisés.
def deviner_nombre(n) :
Question 2 - Écrire la fonction deviner_nombre_automatique qui prend un nombre entier en paramètre. Cette fonction effectue le fonctionnement inverse de la fonction.
Elle tire au hasard un nombre entre 0 et et va essayer de le deviner automatiquement. Le programme fait comme s’il avait oublié la valeur à trouver et essaye de deviner selon la méthode de la dichotomie. La fonction affiche le résultat de la comparaison à chaque étape et renvoie le nombre de coups utilisés.
def deviner_nombre_automatique(n):
¶ Exercice 2 - Dichotomie (version récursive)
Une fonction récursive est une fonction qui s’appelle elle-même. Voici un exemple de fonction récursive de la fonction puissance.
def puissance(n, p):
if p == 0:
return 1
else:
return n* puissance(n, p-1)
Question 1 - Écrire une fonction dichotomie_recursive(t, v) qui implémente l'algorithme de la recherche dichotomique de manière récursive. La fonction True si l'élément cherché est dans la liste, False sinon.
def dichotomie_recursive(t, v):